VC Theoretical Explanation of Double Descent

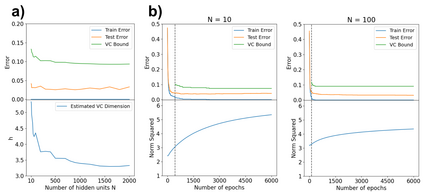
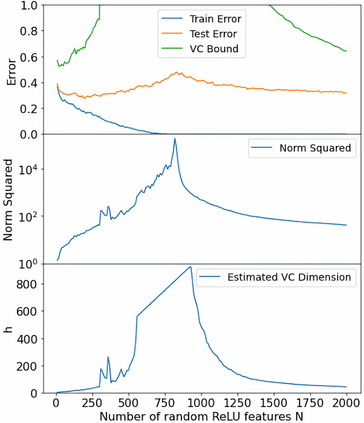
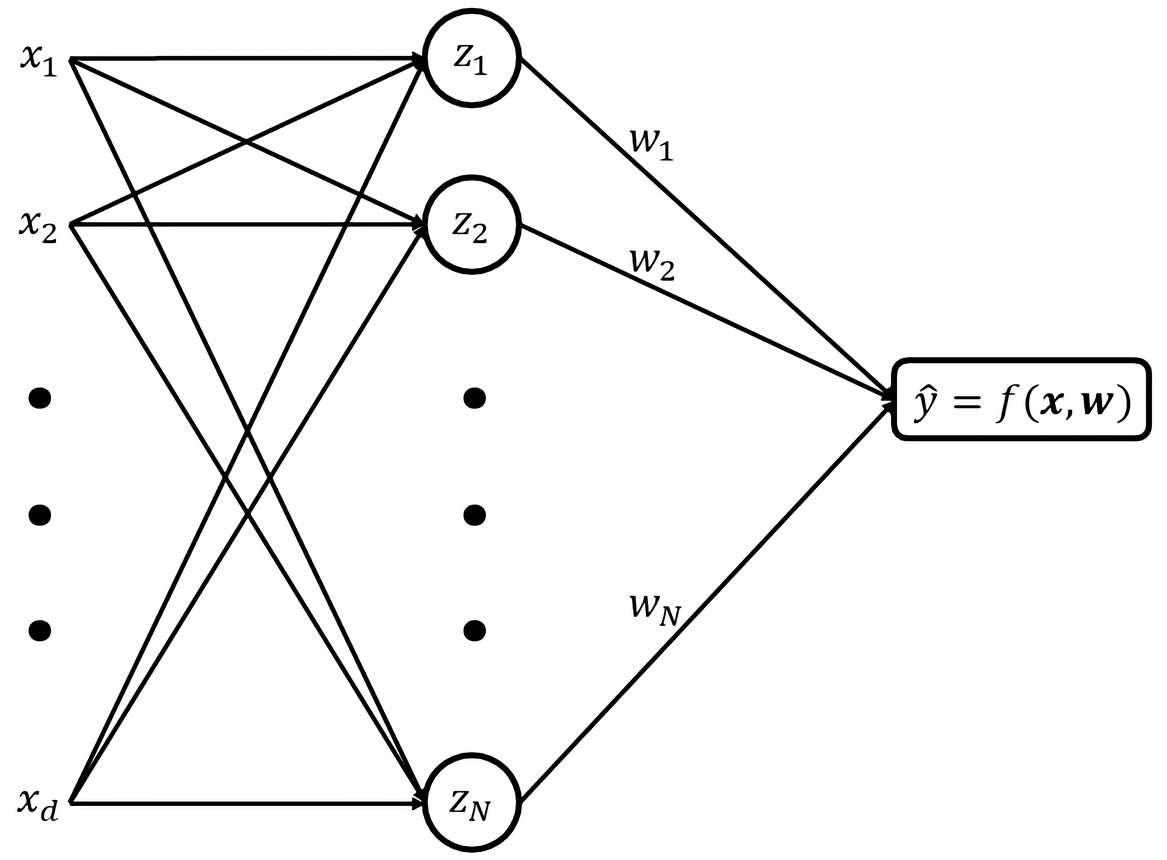
There has been growing interest in generalization performance of large multilayer neural networks that can be trained to achieve zero training error, while generalizing well on test data. This regime is known as 'second descent' and it appears to contradict the conventional view that optimal model complexity should reflect an optimal balance between underfitting and overfitting, i.e., the bias-variance trade-off. This paper presents a VC-theoretical analysis of double descent and shows that it can be fully explained by classical VC-generalization bounds. We illustrate an application of analytic VC-bounds for modeling double descent for classification problems, using empirical results for several learning methods, such as SVM, Least Squares, and Multilayer Perceptron classifiers. In addition, we discuss several reasons for the misinterpretation of VC-theoretical results in Deep Learning community.