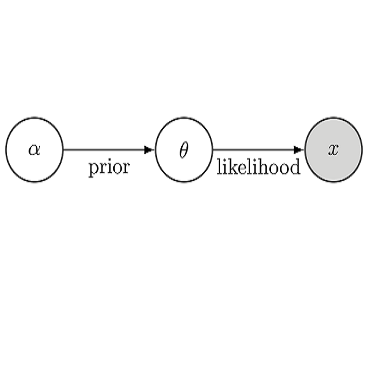
Bayesian inference and kernel methods are well established in machine learning. The neural network Gaussian process in particular provides a concept to investigate neural networks in the limit of infinitely wide hidden layers by using kernel and inference methods. Here we build upon this limit and provide a field-theoretic formalism which covers the generalization properties of infinitely wide networks. We systematically compute generalization properties of linear, non-linear, and deep non-linear networks for kernel matrices with heterogeneous entries. In contrast to currently employed spectral methods we derive the generalization properties from the statistical properties of the input, elucidating the interplay of input dimensionality, size of the training data set, and variability of the data. We show that data variability leads to a non-Gaussian action reminiscent of a ($\varphi^3+\varphi^4$)-theory. Using our formalism on a synthetic task and on MNIST we obtain a homogeneous kernel matrix approximation for the learning curve as well as corrections due to data variability which allow the estimation of the generalization properties and exact results for the bounds of the learning curves in the case of infinitely many training data points.
翻译:暂无翻译