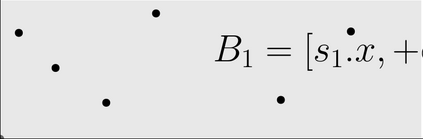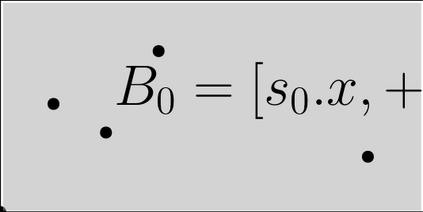In the two-dimensional orthogonal colored range counting problem, we preprocess a set, $P$, of $n$ colored points on the plane, such that given an orthogonal query rectangle, the number of distinct colors of the points contained in this rectangle can be computed efficiently. For this problem, we design three new solutions, and the bounds of each can be expressed in some form of time-space tradeoff. By setting appropriate parameter values for these solutions, we can achieve new specific results with (the space are in words and $\epsilon$ is an arbitrary constant in $(0,1)$): ** $O(n\lg^3 n)$ space and $O(\sqrt{n}\lg^{5/2} n \lg \lg n)$ query time; ** $O(n\lg^2 n)$ space and $O(\sqrt{n}\lg^{4+\epsilon} n)$ query time; ** $O(n\frac{\lg^2 n}{\lg \lg n})$ space and $O(\sqrt{n}\lg^{5+\epsilon} n)$ query time; ** $O(n\lg n)$ space and $O(n^{1/2+\epsilon})$ query time. A known conditional lower bound to this problem based on Boolean matrix multiplication gives some evidence on the difficulty of achieving near-linear space solutions with query time better than $\sqrt{n}$ by more than a polylogarithmic factor using purely combinatorial approaches. Thus the time and space bounds in all these results are efficient. Previously, among solutions with similar query times, the most space-efficient solution uses $O(n\lg^4 n)$ space to answer queries in $O(\sqrt{n}\lg^8 n)$ time (SIAM. J. Comp.~2008). Thus the new results listed above all achieve improvements in space efficiency, while all but the last result achieve speed-up in query time as well.
翻译:在双维或线性色范围计数问题中, 我们预处理一套, $P$, 在平面上的彩色点数为 $n 。 在正方形查询矩形中, 可以有效计算出此矩形中各点不同颜色的数量。 对于这个问题, 我们设计了三种新的解决方案, 并且每种的界限都可以以某种时间空间交换方式表达。 通过为这些解决方案设定适当的参数值, 我们可以实现新的具体结果 ( 空间是用字数表示, 美元是任意的, 美元是用$( 0. 1 美元): ** (n\ g3 n) 彩色查询矩形, 和 $( g\ g/2) 圆矩形的彩色点数 。 (n) 空间和 $( sqrentrick} 时间( lQ) 时间( m) 新的 时间( liqrent) =( lic) 时间( likelex) 问题是用 N. (n\\\\\ lix) lexn mocal=n yal romodeal modeal=n; (n=n) ral=n=n=n=n=n=n=oxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx