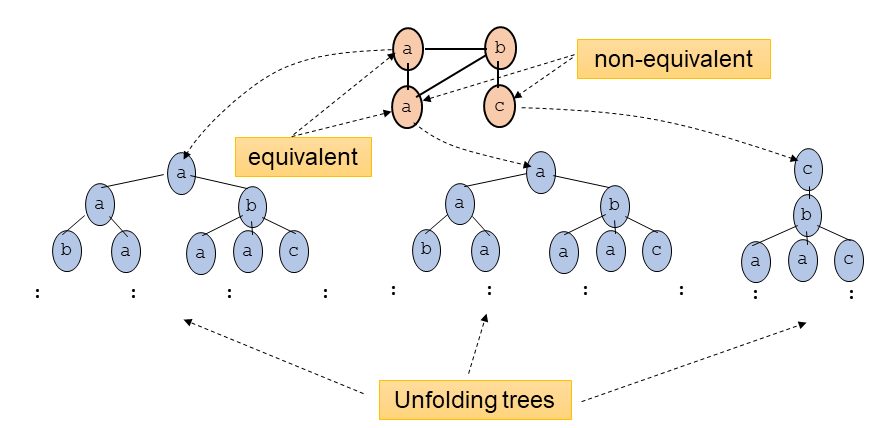
Graph Neural Networks (GNNs) are a wide class of connectionist models for graph processing. They perform an iterative message passing operation on each node and its neighbors, to solve classification/ clustering tasks -- on some nodes or on the whole graph -- collecting all such messages, regardless of their order. Despite the differences among the various models belonging to this class, most of them adopt the same computation scheme, based on a local aggregation mechanism and, intuitively, the local computation framework is mainly responsible for the expressive power of GNNs. In this paper, we prove that the Weisfeiler--Lehman test induces an equivalence relationship on the graph nodes that exactly corresponds to the unfolding equivalence, defined on the original GNN model. Therefore, the results on the expressive power of the original GNNs can be extended to general GNNs which, under mild conditions, can be proved capable of approximating, in probability and up to any precision, any function on graphs that respects the unfolding equivalence.
翻译:神经网络图( GNNS) 是用于图形处理的广泛的连接模型。 它们在每个节点及其周边进行迭接信息传递操作, 以解决分类/ 集群任务 -- -- 在某些节点上或整个图上 -- -- 收集所有这类信息, 不论其顺序如何。 尽管属于该类的不同模型之间存在差异, 但大多数模型采用相同的计算方法, 以本地聚合机制为基础, 直观地说, 本地计算框架主要负责 GNS 的表达力 。 在本文中, 我们证明 Weisfeiler- Lehman 测试在图形节点上产生了与原始 GNN 模型定义的正向等值完全对应的等值关系 。 因此, 原始 GNNs 的表达力结果可以推广到普通 GNNs, 在温和的条件下, 可以证明在尊重正在形成的等值的图形上的任何功能都能够适应、 概率和精确度。