Fast Algorithm for Constrained Linear Inverse Problems

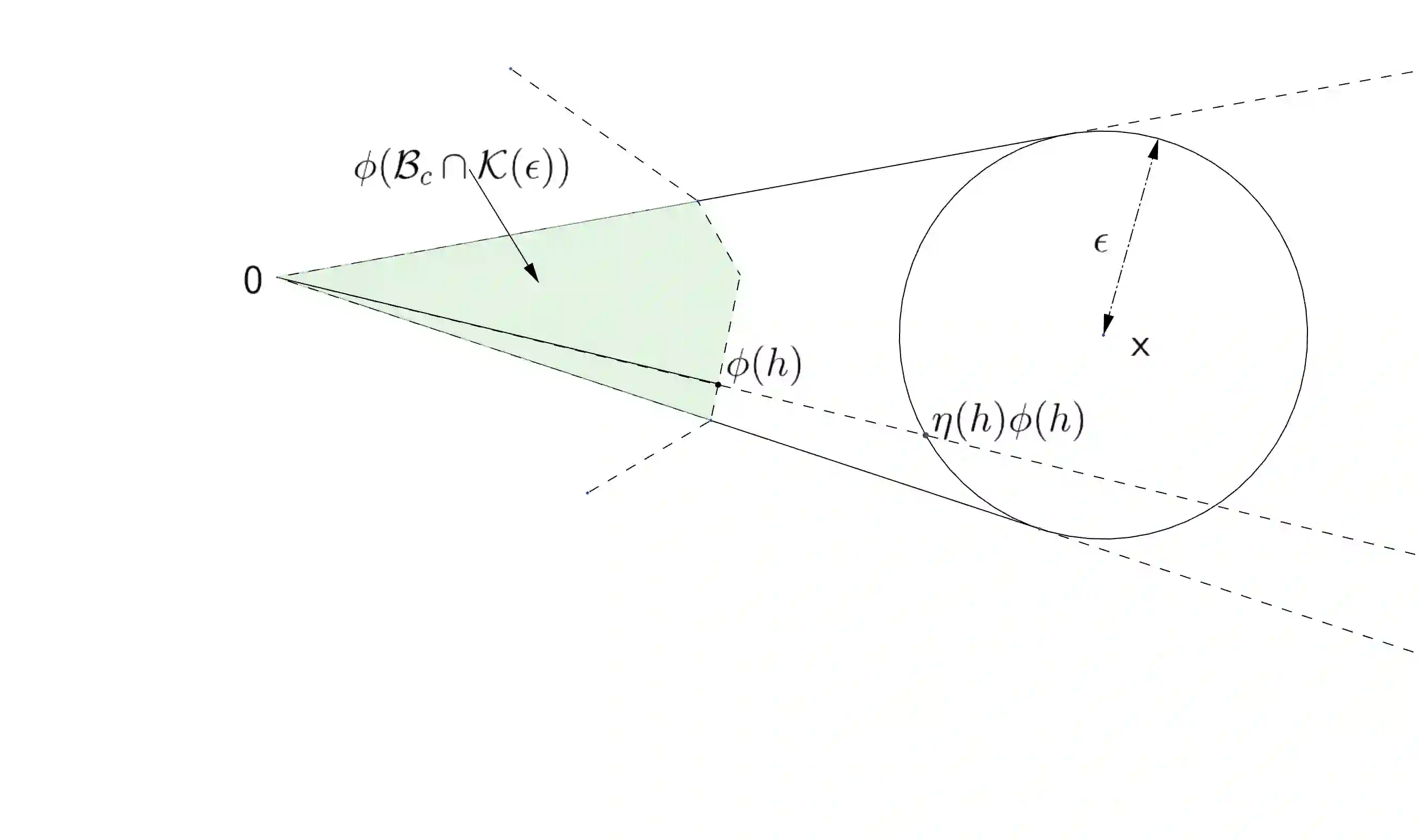
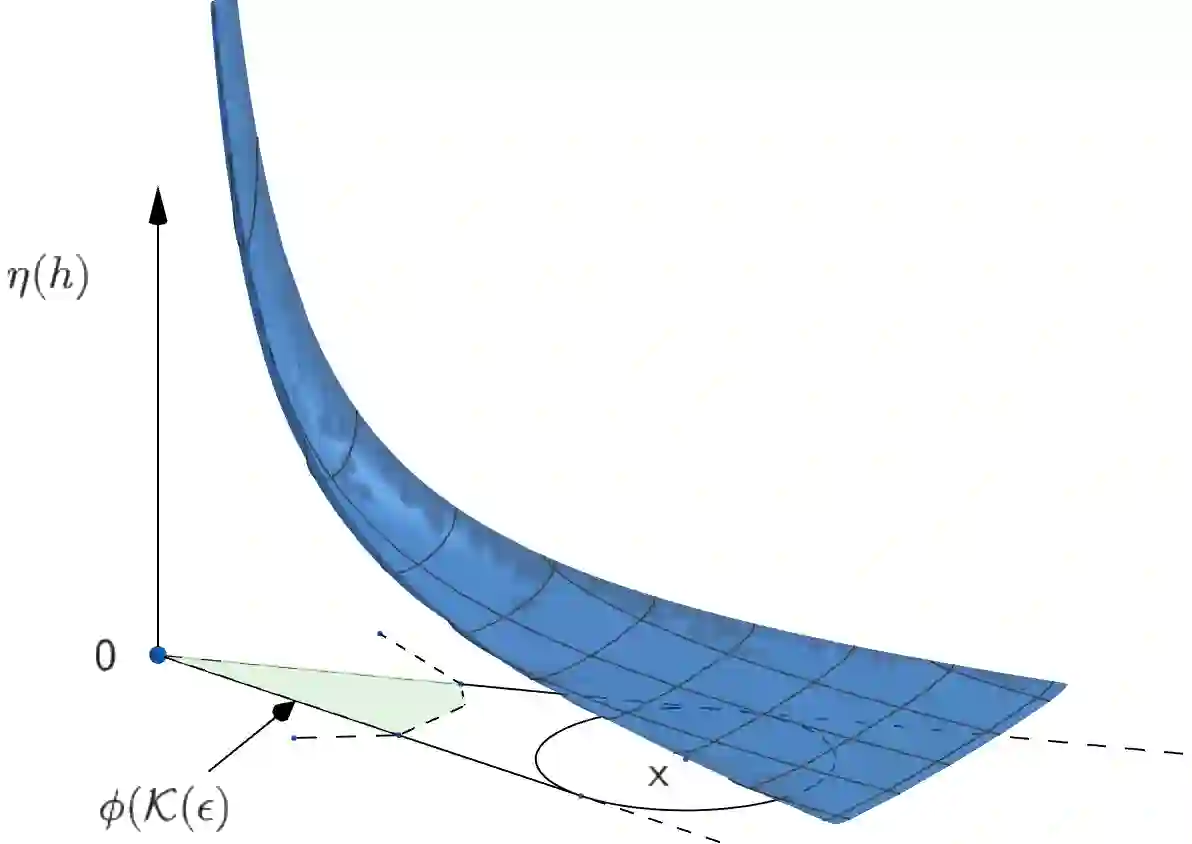
We consider the constrained Linear Inverse Problem (LIP), where a certain atomic norm (like the $\ell_1 $ norm) is minimized subject to a quadratic constraint. Typically, such cost functions are non-differentiable which makes them not amenable to the fast optimization methods existing in practice. We propose two equivalent reformulations of the constrained LIP with improved convex regularity: (i) a smooth convex minimization problem, and (ii) a strongly convex min-max problem. These problems could be solved by applying existing acceleration-based convex optimization methods which provide better $ O \left( \frac{1}{k^2} \right) $ theoretical convergence guarantee, improving upon the current best rate of $ O \left( \frac{1}{k} \right) $. We also provide a novel algorithm named the Fast Linear Inverse Problem Solver (FLIPS), which is tailored to maximally exploit the structure of the reformulations. We demonstrate the performance of FLIPS on the classical problems of Binary Selection, Compressed Sensing, and Image Denoising. We also provide open source \texttt{MATLAB} package for these three examples, which can be easily adapted to other LIPs.