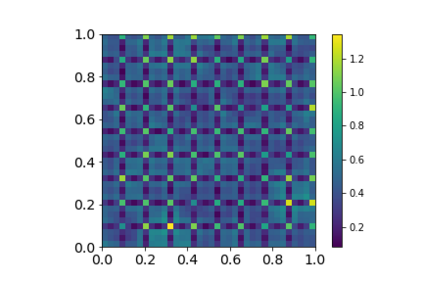
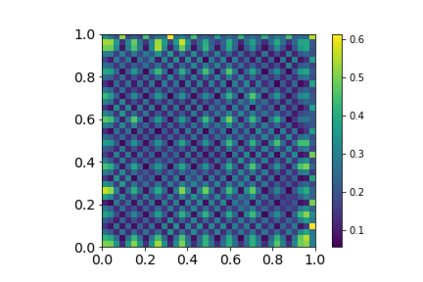
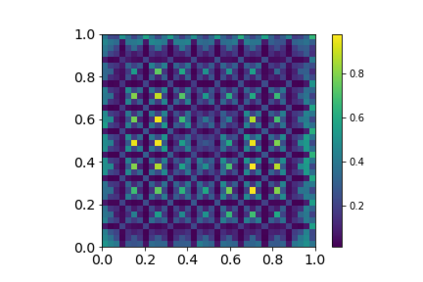
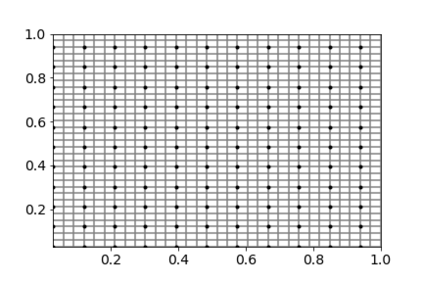
In the Big Data era, with the ubiquity of geolocation sensors in particular, massive datasets exhibiting a possibly complex spatial dependence structure are becoming increasingly available. In this context, the standard probabilistic theory of statistical learning does not apply directly and guarantees of the generalization capacity of predictive rules learned from such data are left to establish. We analyze here the simple Kriging task, the flagship problem in Geostatistics: the values of a square integrable random field $X=\{X_s\}_{s\in S}$, $S\subset \mathbb{R}^2$, with unknown covariance structure are to be predicted with minimum quadratic risk, based upon observing a single realization of the spatial process at a finite number of locations $s_1,\; \ldots,\; s_n$ in $S$. Despite the connection of this minimization problem with kernel ridge regression, establishing the generalization capacity of empirical risk minimizers is far from straightforward, due to the non i.i.d. nature of the spatial data $X_{s_1},\; \ldots,\; X_{s_n}$ involved. In this article, nonasymptotic bounds of order $O_{\mathbb{P}}(1/n)$ are proved for the excess risk of a plug-in predictive rule mimicking the true minimizer in the case of isotropic stationary Gaussian processes observed at locations forming a regular grid. These theoretical results, as well as the role played by the technical conditions required to establish them, are illustrated by various numerical experiments and hopefully pave the way for further developments in statistical learning based on spatial data.
翻译:在大数据时代,随着地理定位传感器的无处不在,大规模数据集正日益呈现出可能复杂的空间依赖结构。在这方面,统计学习的标准概率学理论并不直接适用,保证从这些数据中学得的预测规则的普遍化能力有待于确定。我们在这里分析简单的克里吉任务,即地理统计学中的最重要的问题:平方随机字段的数值$X{X_s_s ⁇ s\in S}$, $S\subset\mathb{R ⁇ 2$, 且空间数据常态结构不明的超额空间数据集将面临最小的二次风险。 在一定数量的地点观测空间过程的单一实现情况 $_1,\\\; 焊多,\ s_nS$。 尽管这种最小化问题与内脊后退有关, 建立实验风险最小化的能力远非直截然, 但由于空间数据的性质 $X_r_r_1} 定期变异位结构结构结构的预测, 也以定期变数为最低值。