Testing for long-range dependence in non-stationary time series time-varying regression

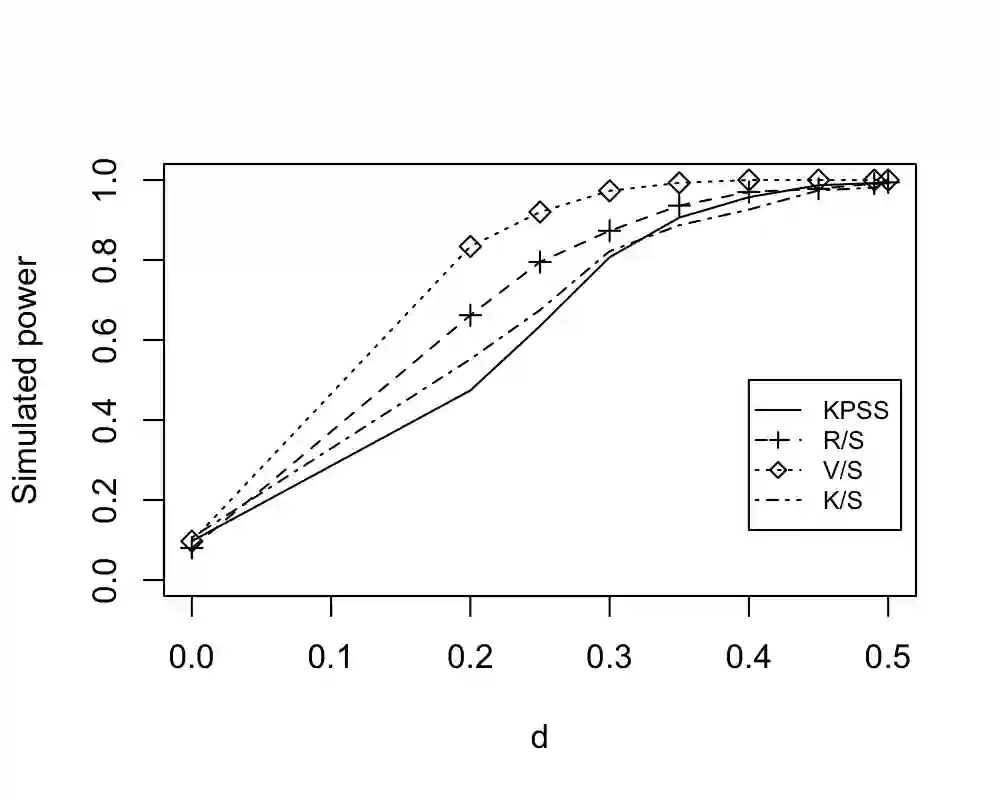
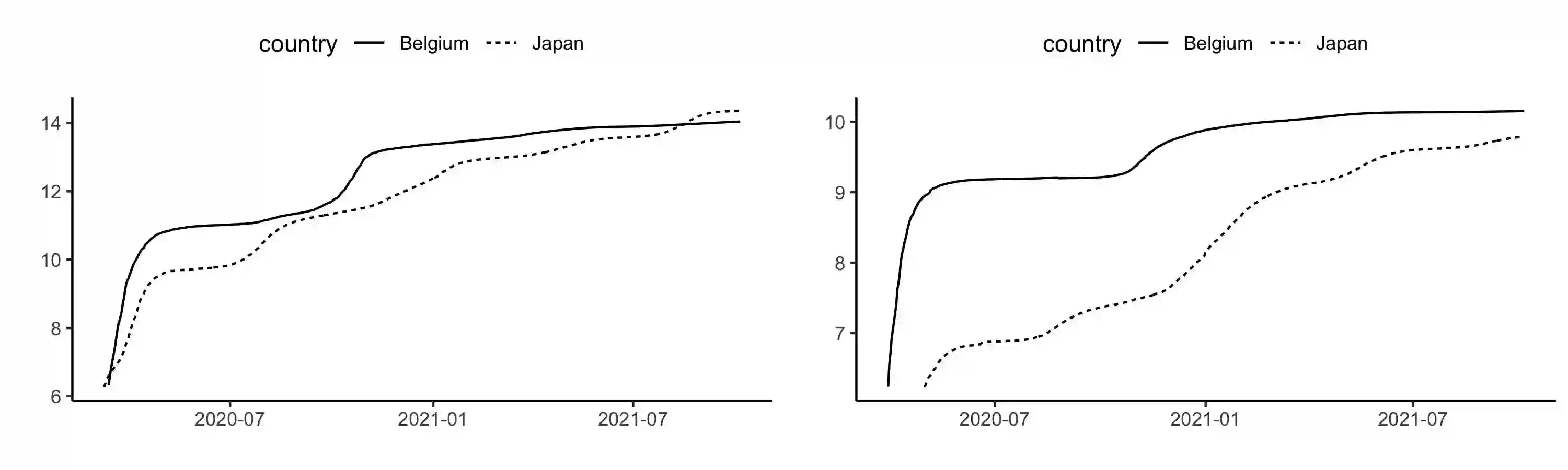
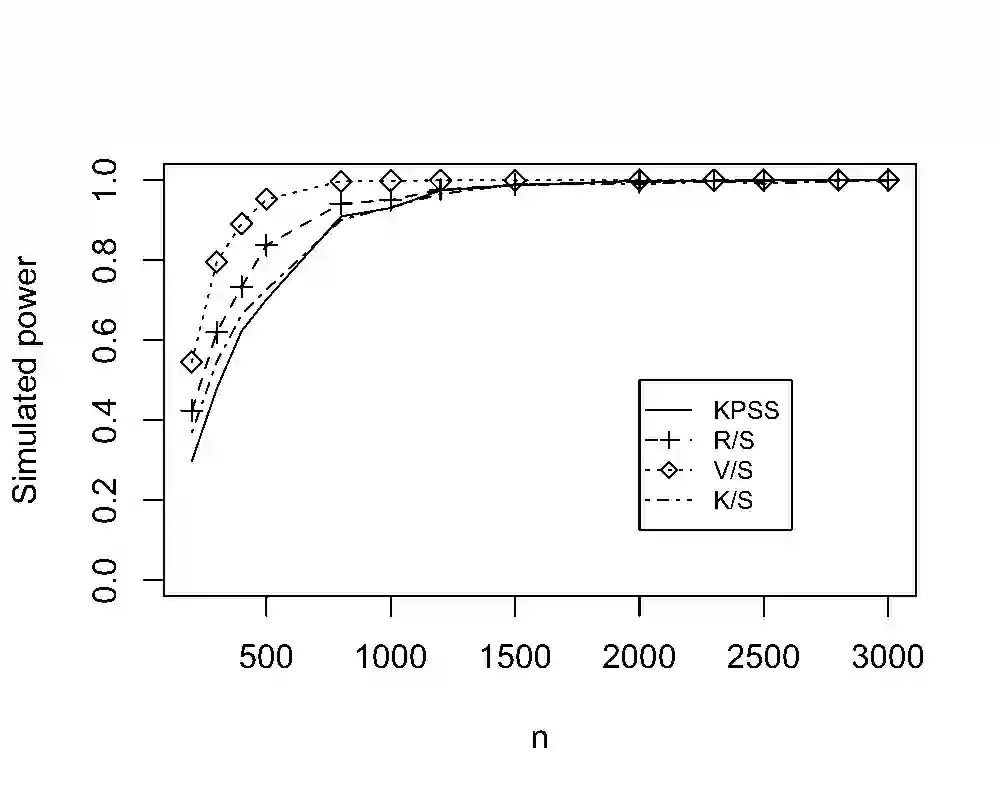
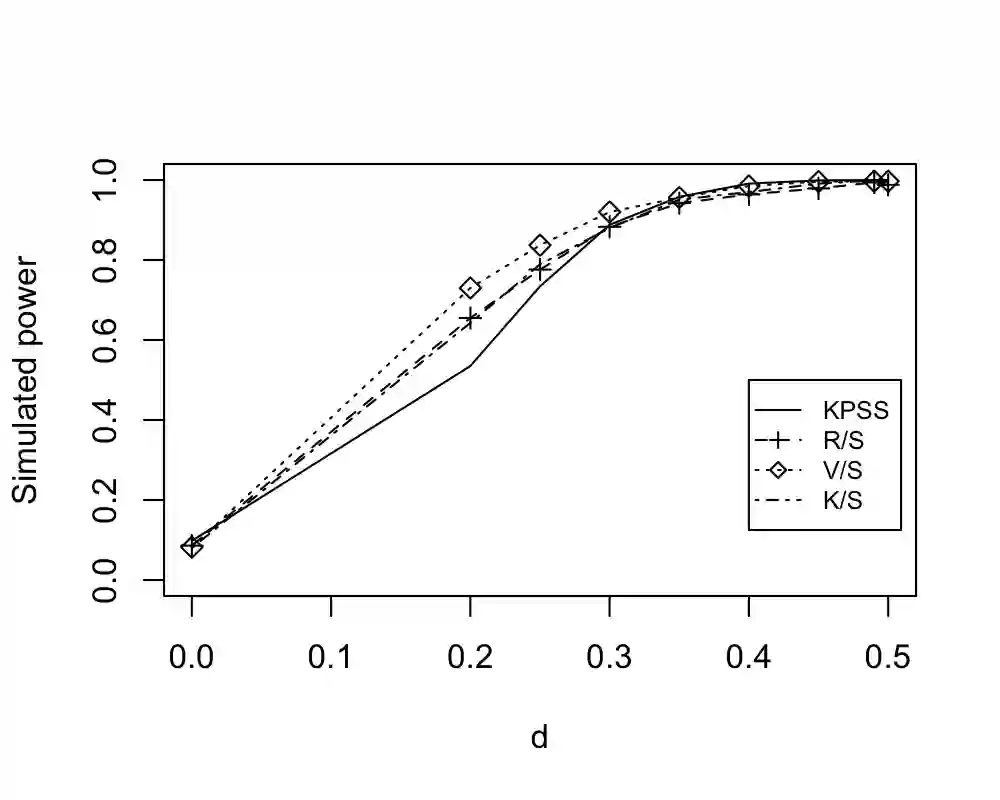
We consider the problem of testing for long-range dependence for time-varying coefficient regression models. The covariates and errors are assumed to be locally stationary, which allows complex temporal dynamics and heteroscedasticity. We develop KPSS, R/S, V/S, and K/S-type statistics based on the nonparametric residuals, and propose bootstrap approaches equipped with a difference-based long-run covariance matrix estimator for practical implementation. Under the null hypothesis, the local alternatives as well as the fixed alternatives, we derive the limiting distributions of the test statistics, establish the uniform consistency of the difference-based long-run covariance estimator, and justify the bootstrap algorithms theoretically. In particular, the exact local asymptotic power of our testing procedure enjoys the order $O( \log^{-1} n)$, the same as that of the classical KPSS test for long memory in strictly stationary series without covariates. We demonstrate the effectiveness of our tests by extensive simulation studies. The proposed tests are applied to a COVID-19 dataset in favor of long-range dependence in the cumulative confirmed series of COVID-19 in several countries, and to the Hong Kong circulatory and respiratory dataset, identifying a new type of 'spurious long memory'.