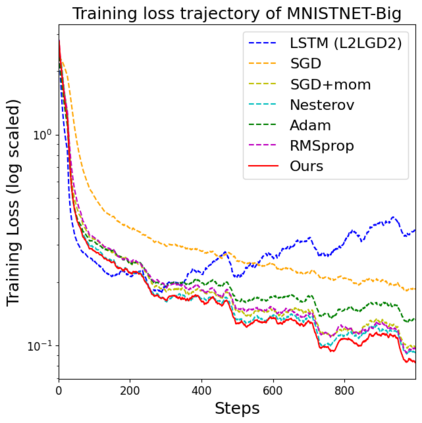
Efficient Non-Parametric Optimizer Search for Diverse Tasks

Efficient and automated design of optimizers plays a crucial role in full-stack AutoML systems. However, prior methods in optimizer search are often limited by their scalability, generability, or sample efficiency. With the goal of democratizing research and application of optimizer search, we present the first efficient, scalable and generalizable framework that can directly search on the tasks of interest. We first observe that optimizer updates are fundamentally mathematical expressions applied to the gradient. Inspired by the innate tree structure of the underlying math expressions, we re-arrange the space of optimizers into a super-tree, where each path encodes an optimizer. This way, optimizer search can be naturally formulated as a path-finding problem, allowing a variety of well-established tree traversal methods to be used as the search algorithm. We adopt an adaptation of the Monte Carlo method to tree search, equipped with rejection sampling and equivalent- form detection that leverage the characteristics of optimizer update rules to further boost the sample efficiency. We provide a diverse set of tasks to benchmark our algorithm and demonstrate that, with only 128 evaluations, the proposed framework can discover optimizers that surpass both human-designed counterparts and prior optimizer search methods.