Fasano-Franceschini Test: an Implementation of a 2-Dimensional Kolmogorov-Smirnov test in R

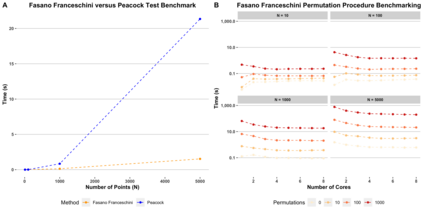
The univariate Kolmogorov-Smirnov (KS) test is a non-parametric statistical test designed to assess whether two samples come from the same underlying distribution. The versatility of the KS test has made it a cornerstone of statistical analysis across the scientific disciplines. However, the test proposed by Kolmogorov and Smirnov does not naturally extend to multidimensional distributions. Here, we present the fasano.franceschini.test package, an R implementation of the 2-D KS two-sample test as defined by Fasano and Franceschini (Fasano and Franceschini 1987) and provide multiple use cases across the scientific disciplines. The fasano.franceschini.test package provides three improvements over the current 2-D KS test on the Comprehensive R Archive Network (CRAN): (i) the Fasano and Franceschini test has been shown to run in $O(n^2)$ versus the Peacock implementation which runs in $O(n^3)$; (ii) the package implements a procedure for handling ties in the data; and (iii) the package implements a parallelized permutation procedure for improved significance testing. Ultimately, the fasano.franceschini.test package presents a robust statistical test for analyzing random samples defined in 2-dimensions.