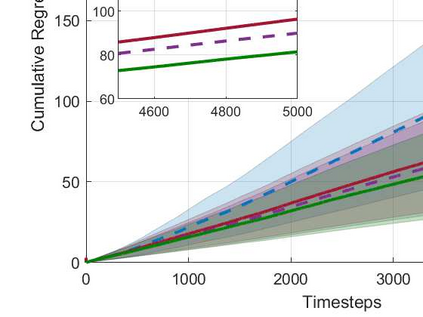
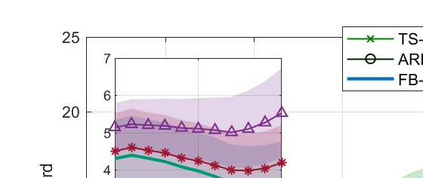
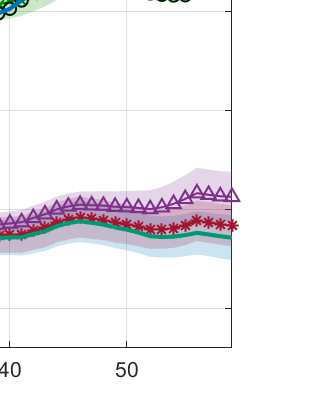
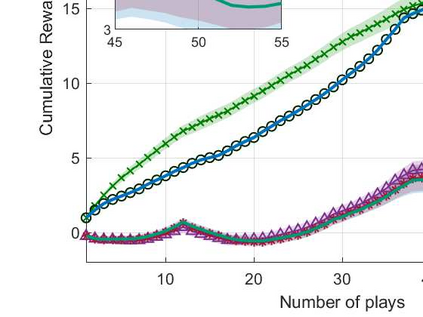
We consider the non-stationary multi-armed bandit (MAB) framework and propose a Kolmogorov-Smirnov (KS) test based Thompson Sampling (TS) algorithm named TS-KS, that actively detects change points and resets the TS parameters once a change is detected. In particular, for the two-armed bandit case, we derive bounds on the number of samples of the reward distribution to detect the change once it occurs. Consequently, we show that the proposed algorithm has sub-linear regret. Contrary to existing works, our algorithm is able to detect a change when the underlying reward distribution changes even though the mean reward remains the same. Finally, to test the efficacy of the proposed algorithm, we employ it in two case-studies: i) task-offloading scenario in wireless edge-computing, and ii) portfolio optimization. Our results show that the proposed TS-KS algorithm outperforms not only the static TS algorithm but also it performs better than other bandit algorithms designed for non-stationary environments. Moreover, the performance of TS-KS is at par with the state-of-the-art forecasting algorithms such as Facebook-PROPHET and ARIMA.
翻译:我们考虑的是非静止多武装匪徒框架,并提议一个基于Kolmogorov-Smirnov(KS)测试的Thompson抽样算法,名为TS-KS,该算法在发现变化后积极检测变化点并重置TS参数。特别是,对于两武装匪徒案,我们从奖励分配的样本数量中得出界限,以在变化发生时发现变化。因此,我们表明,提议的算法有亚线性遗憾。与现有工作相反,我们的算法能够在基本报酬分配变化时发现变化,即使平均报酬保持不变。最后,为了测试拟议算法的效力,我们在两个案例研究中使用了这个算法:一是无线边置和组合优化的任务卸载情景。我们的结果显示,拟议的TS-KS算法不仅显示静态TS算法,而且比为非静止环境设计的其他波测算法还表现得更好。此外,TS-KS和FFAMAS在状态上的状态预测和APRMAS的状态。