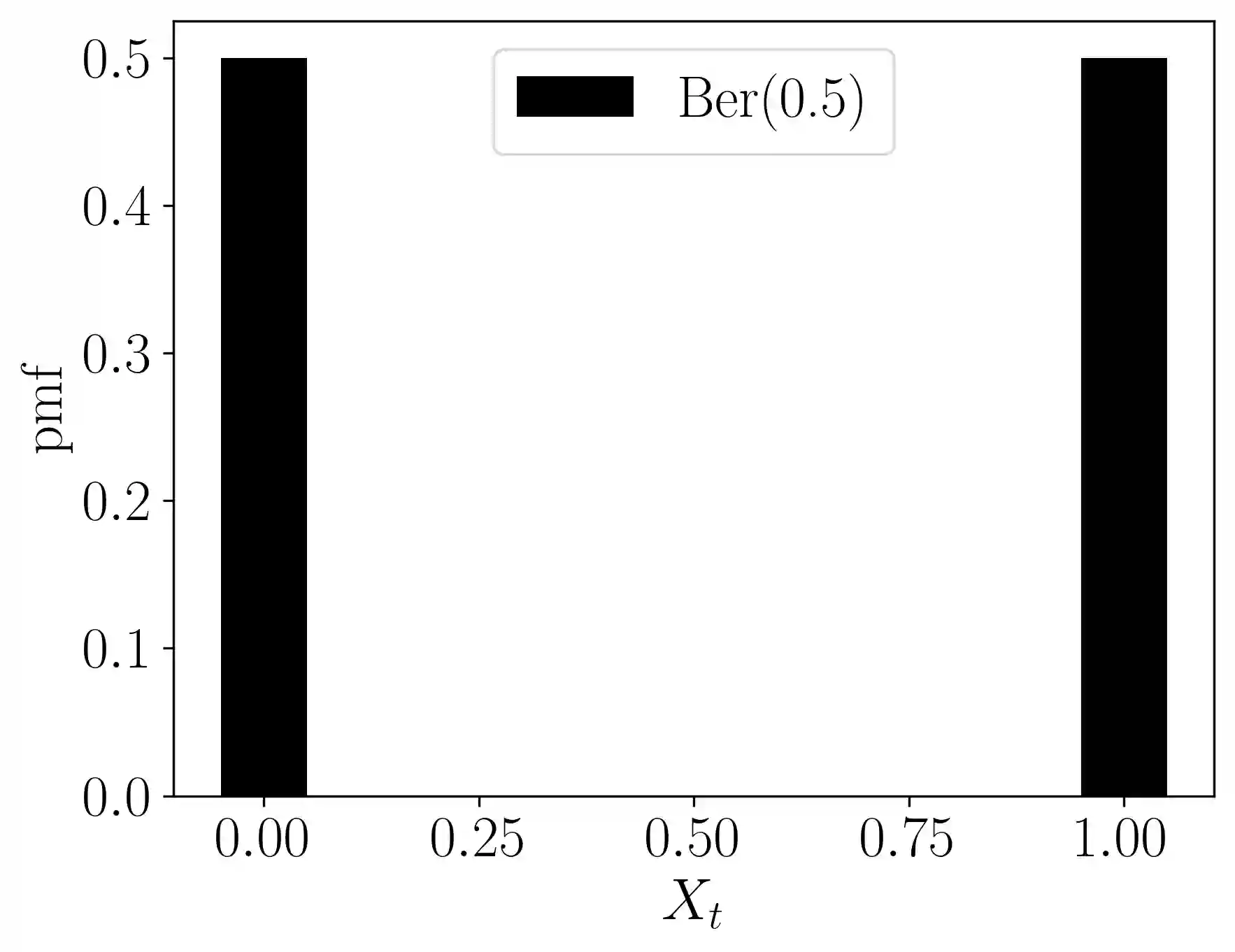
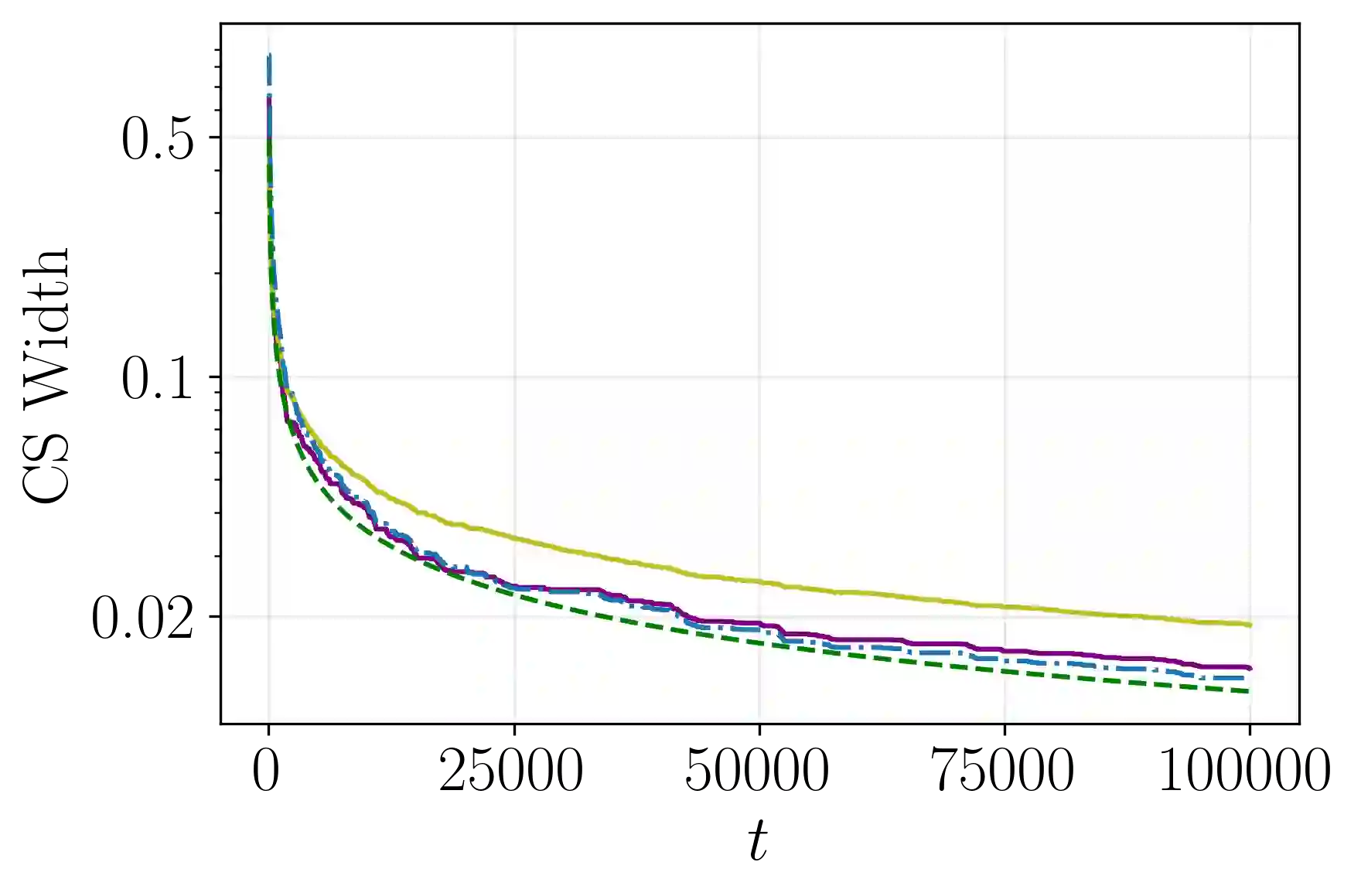
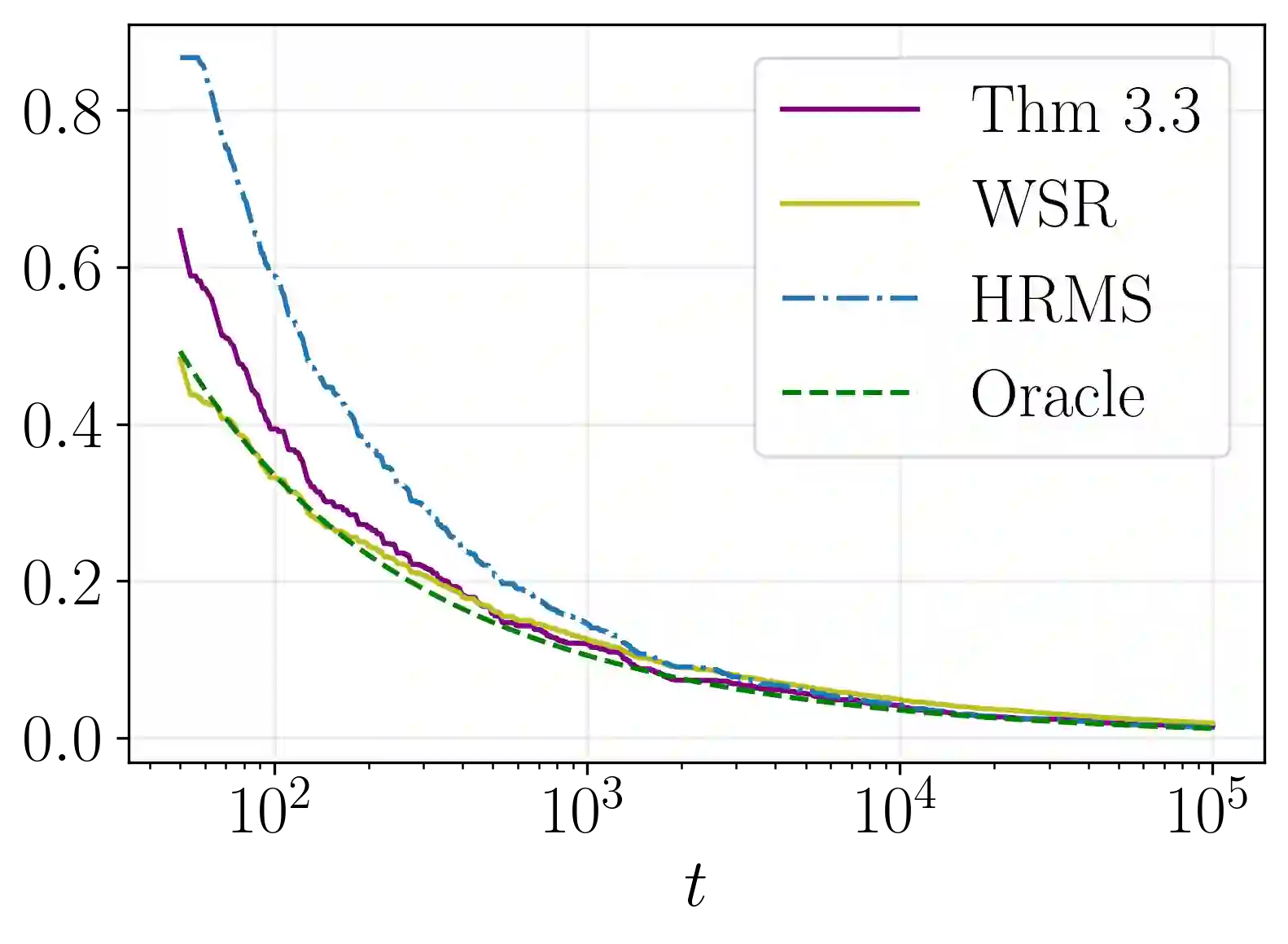
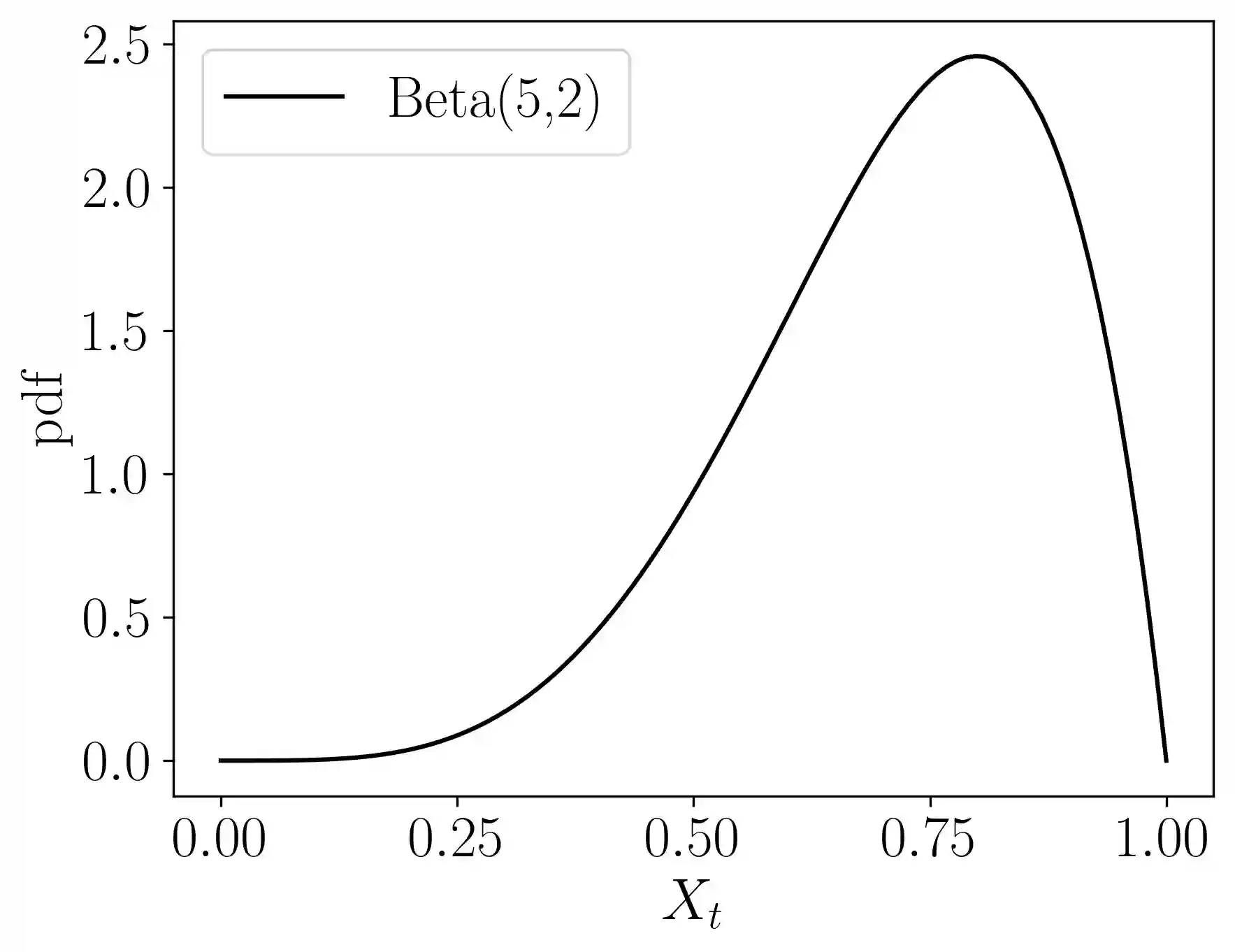
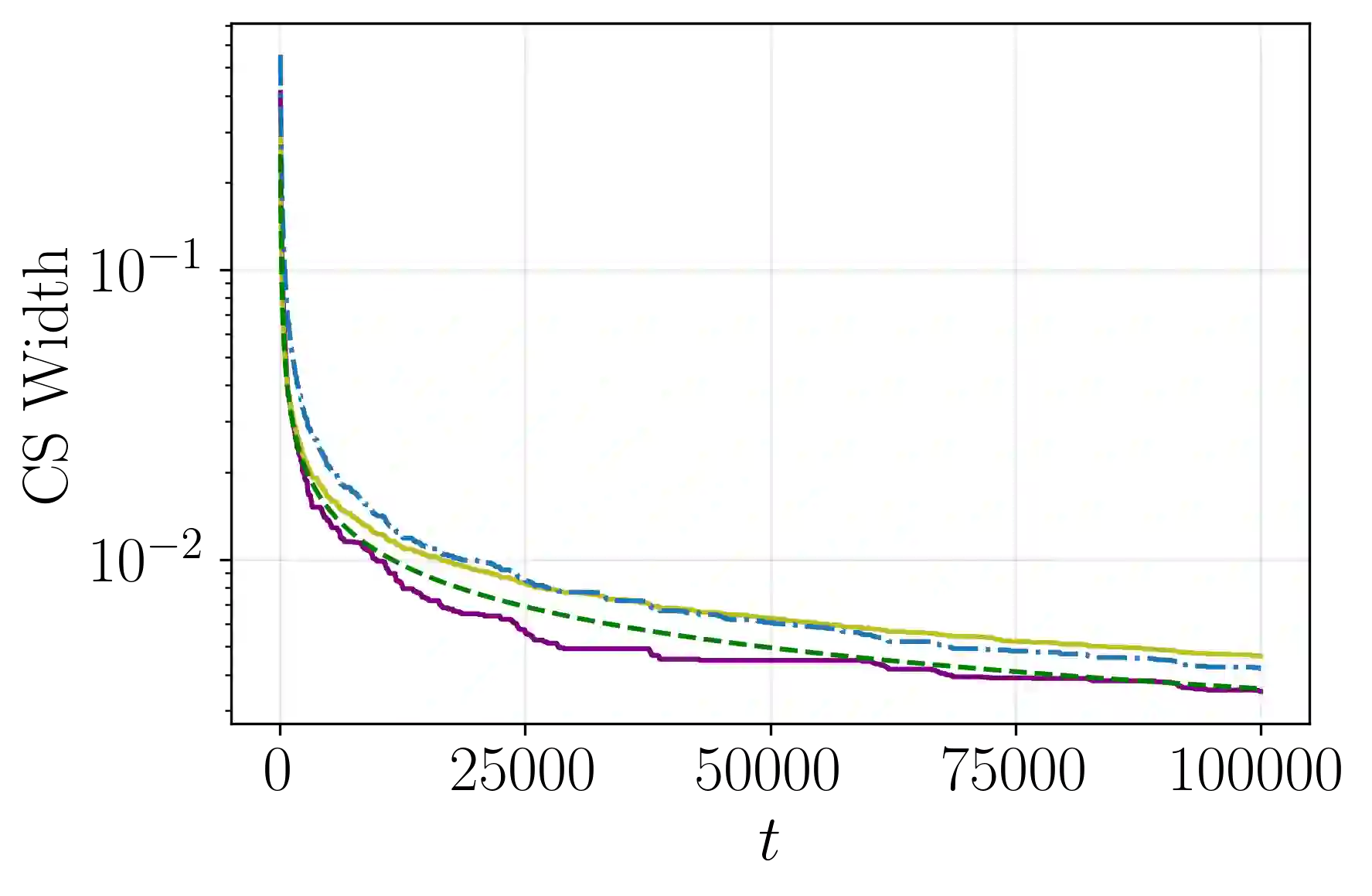
We derive a new closed-form variance-adaptive confidence sequence (CS) for estimating the average conditional mean of a sequence of bounded random variables. Empirically, it yields the tightest closed-form CS we have found for tracking time-varying means, across sample sizes up to $\approx 10^6$. When the observations happen to have the same conditional mean, our CS is asymptotically tighter than the recent closed-form CS of Waudby-Smith and Ramdas [38]. It also has other desirable properties: it is centered at the unweighted sample mean and has limiting width (multiplied by $\sqrt{t/\log t}$) independent of the significance level. We extend our results to provide a CS with the same properties for random matrices with bounded eigenvalues.
翻译:本文推导了一种新的闭式方差自适应置信序列(CS),用于估计有界随机变量序列的条件均值平均值。经验表明,该置信序列在样本量高达约$10^6$的范围内,为追踪时变均值提供了我们所发现的最紧致的闭式CS。当观测值恰好具有相同条件均值时,我们的CS渐近地紧于Waudby-Smith和Ramdas[38]最近提出的闭式CS。该置信序列还具有其他理想特性:以未加权样本均值为中心,且其极限宽度(乘以$\sqrt{t/\log t}$)与显著性水平无关。我们将结果扩展至有界特征值随机矩阵,提供了具有相同性质的CS。