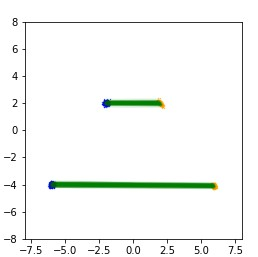
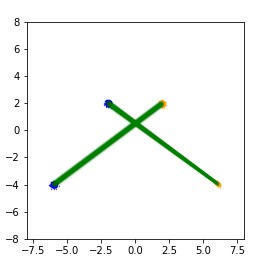
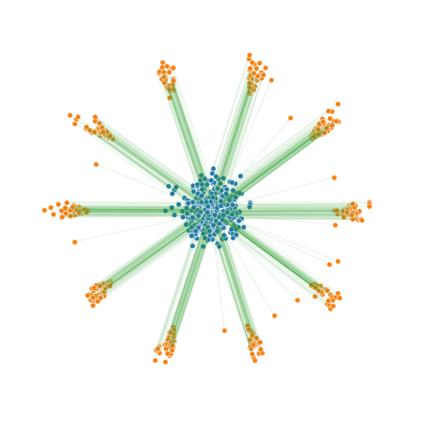
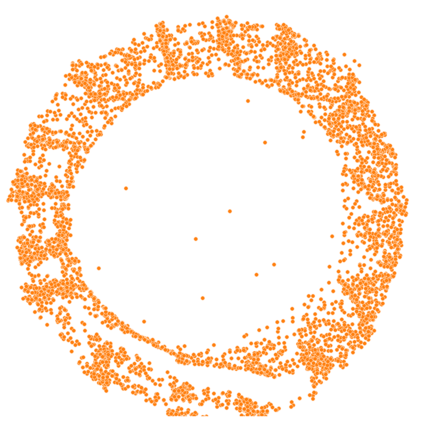
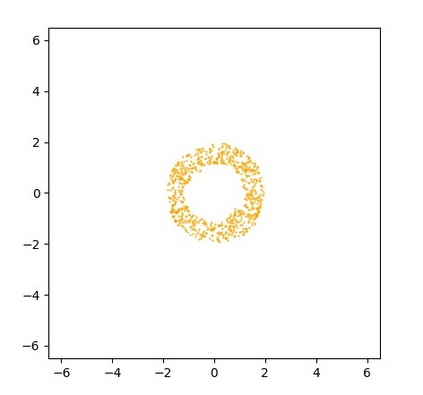
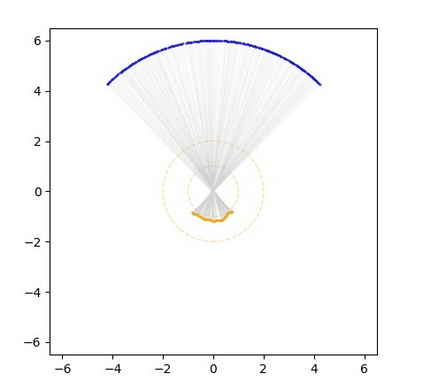
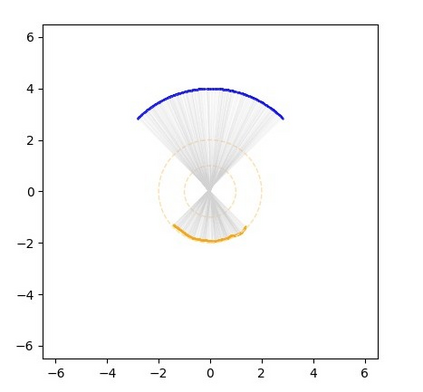
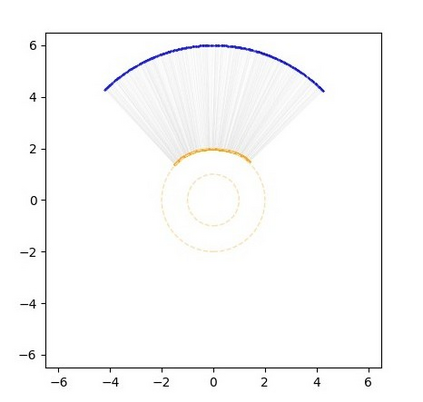
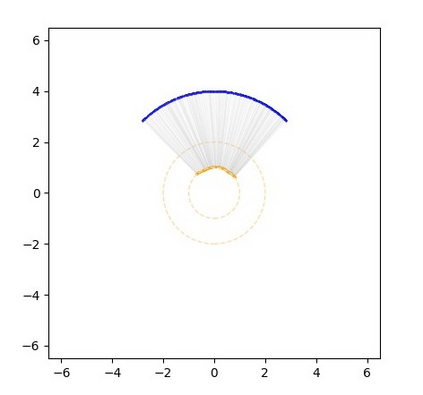
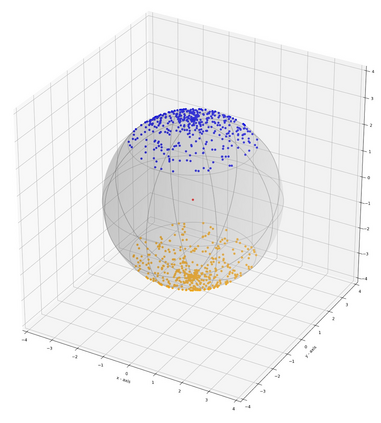
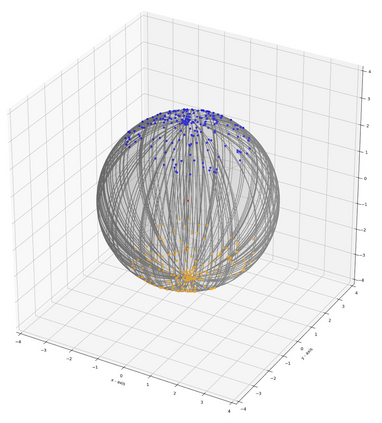
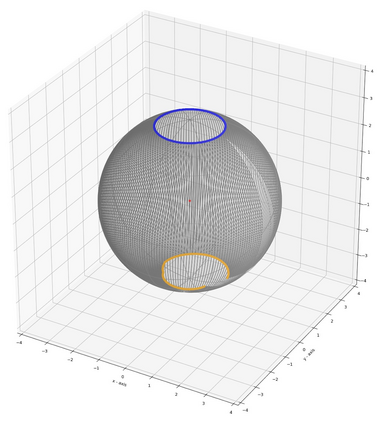
Monge map refers to the optimal transport map between two probability distributions and provides a principled approach to transform one distribution to another. In spite of the rapid developments of the numerical methods for optimal transport problems, computing the Monge maps remains challenging, especially for high dimensional problems. In this paper, we present a scalable algorithm for computing the Monge map between two probability distributions. Our algorithm is based on a weak form of the optimal transport problem, thus it only requires samples from the marginals instead of their analytic expressions, and can accommodate optimal transport between two distributions with different dimensions. Our algorithm is suitable for general cost functions, compared with other existing methods for estimating Monge maps using samples, which are usually for quadratic costs. The performance of our algorithms is demonstrated through a series of experiments with both synthetic and realistic data.
翻译:蒙古语地图是指两种概率分布之间的最佳运输地图,它为将一种分布转换为另一种分布提供了原则性方法。尽管最佳运输问题的数字方法迅速发展,但计算蒙古语地图仍然具有挑战性,特别是对于高维问题。在本文中,我们提出了一个在两种概率分布之间计算蒙古语地图的可缩放算法。我们的算法基于一种最优运输问题的微弱形式,因此只需要边缘的样本,而不是其分析表达方式,并且能够适应不同维度的两种分布之间的最佳运输。我们的算法适合一般成本功能,而使用样本估计蒙古语地图的其他现有方法通常是二次成本。我们算法的性能通过一系列的合成和现实数据实验得到证明。