Scan-based immersed isogeometric flow analysis

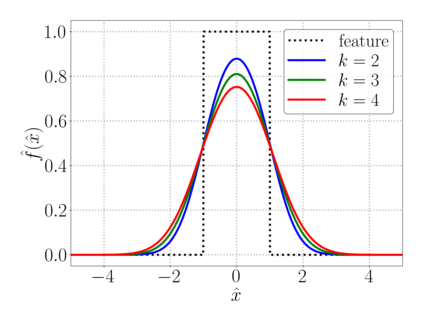
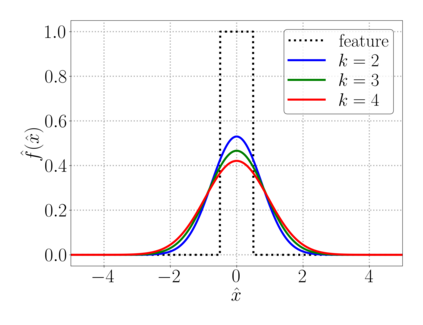
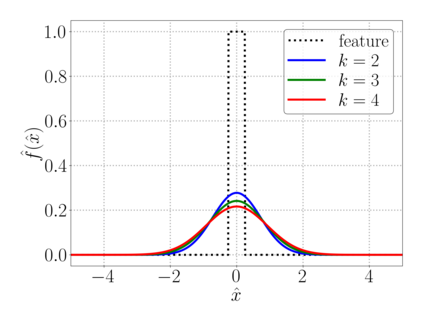
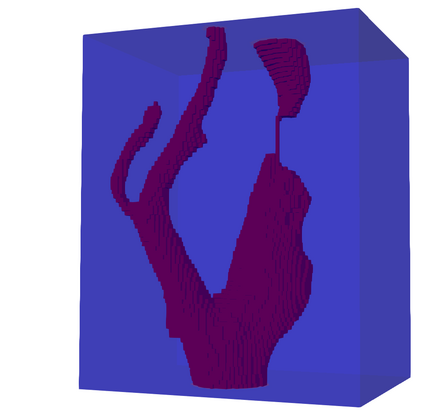
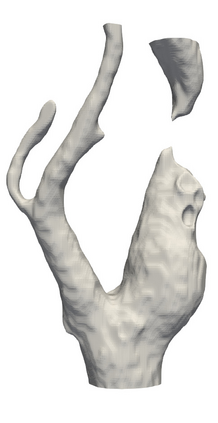
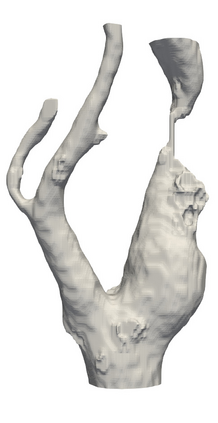
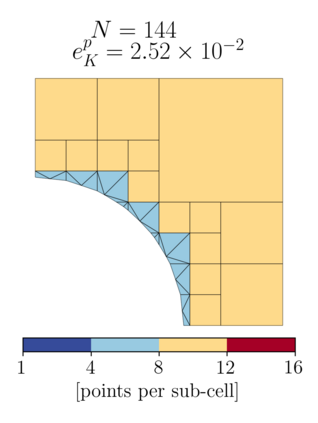
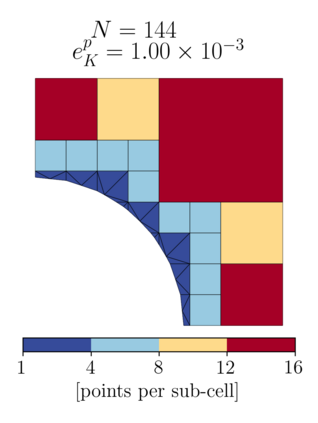
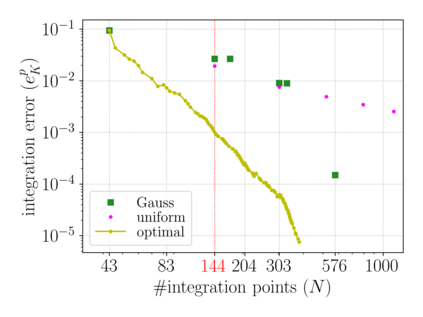
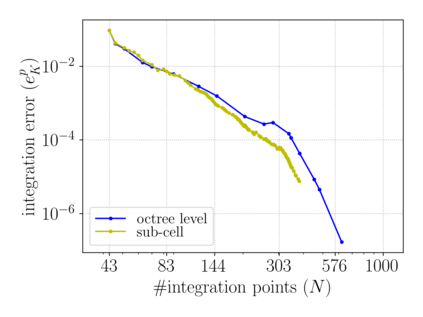
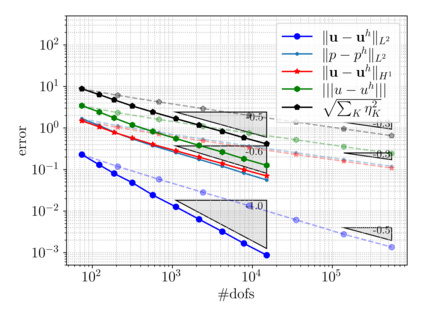
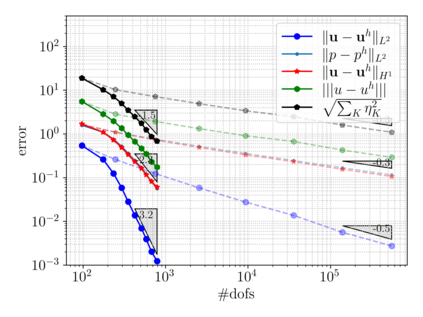
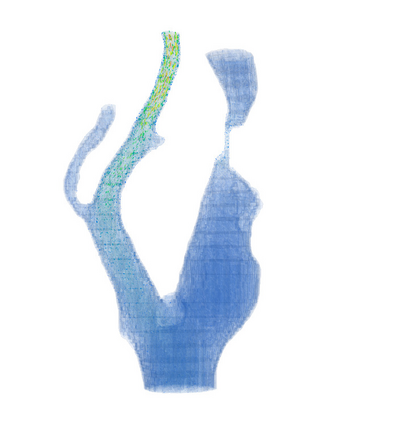
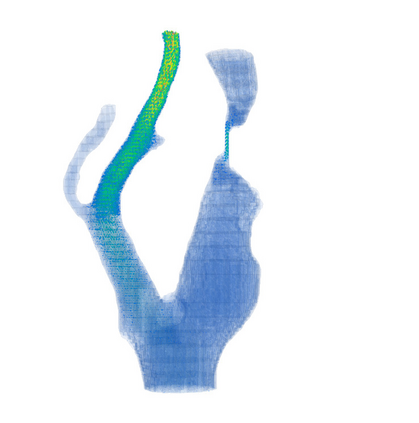
This chapter reviews the work conducted by our team on scan-based immersed isogeometric analysis for flow problems. To leverage the advantageous properties of isogeometric analysis on complex scan-based domains, various innovations have been made: (i) A spline-based segmentation strategy has been developed to extract a geometry suitable for immersed analysis directly from scan data; (ii) A stabilized equal-order velocity-pressure formulation for the Stokes problem has been proposed to attain stable results on immersed domains; (iii) An adaptive integration quadrature procedure has been developed to improve computational efficiency; (iv) A mesh refinement strategy has been developed to capture small features at a priori unknown locations, without drastically increasing the computational cost of the scan-based analysis workflow. We review the key ideas behind each of these innovations, and illustrate these using a selection of simulation results from our work. A patient-specific scan-based analysis case is reproduced to illustrate how these innovations enable the simulation of flow problems on complex scan data.