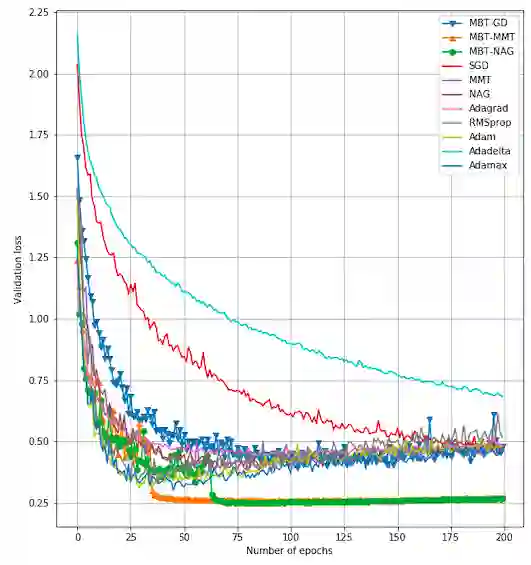
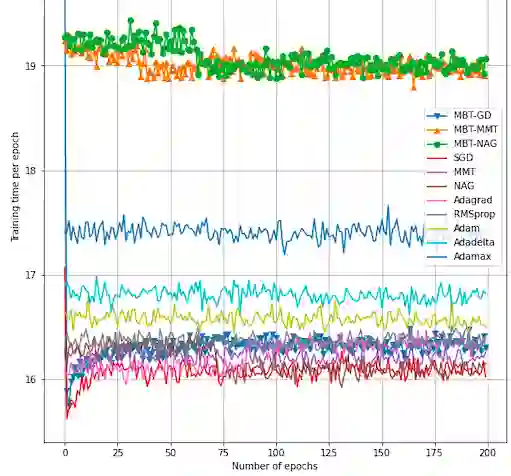
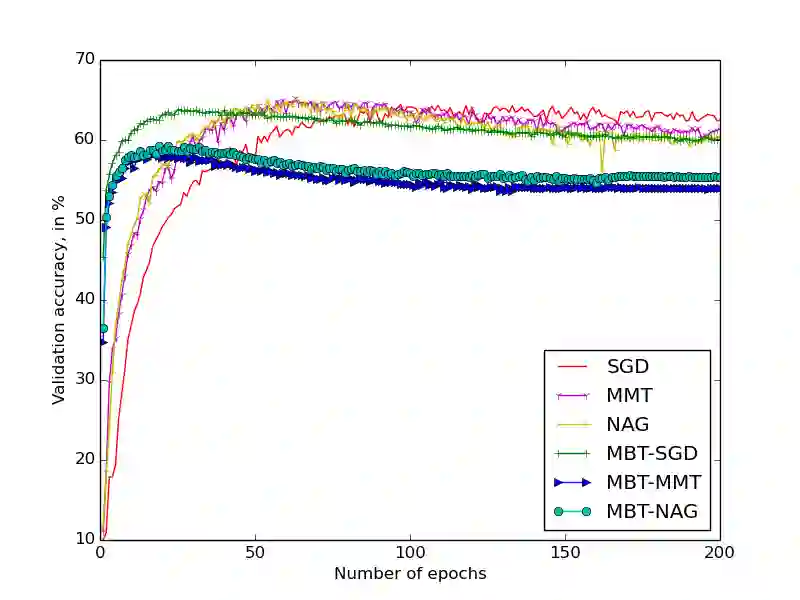
We propose in this paper New Q-Newton's method. The update rule is very simple conceptually, for example $x_{n+1}=x_n-w_n$ where $w_n=pr_{A_n,+}(v_n)-pr_{A_n,-}(v_n)$, with $A_n=\nabla ^2f(x_n)+\delta _n||\nabla f(x_n)||^2.Id$ and $v_n=A_n^{-1}.\nabla f(x_n)$. Here $\delta _n$ is an appropriate real number so that $A_n$ is invertible, and $pr_{A_n,\pm}$ are projections to the vector subspaces generated by eigenvectors of positive (correspondingly negative) eigenvalues of $A_n$. The main result of this paper roughly says that if $f$ is $C^3$ (can be unbounded from below) and a sequence $\{x_n\}$, constructed by the New Q-Newton's method from a random initial point $x_0$, {\bf converges}, then the limit point is a critical point and is not a saddle point, and the convergence rate is the same as that of Newton's method. The first author has recently been successful incorporating Backtracking line search to New Q-Newton's method, thus resolving the convergence guarantee issue observed for some (non-smooth) cost functions. An application to quickly finding zeros of a univariate meromorphic function will be discussed. Various experiments are performed, against well known algorithms such as BFGS and Adaptive Cubic Regularization are presented.
翻译:我们在此纸上提出 New Q- Newton 的方法。 更新规则的概念非常简单, 例如 $x @ n+1 @ x_ x_ n- w_ n$, 其中$w_ n= pr_ a_ n, ⁇ (v_ n)- pr ⁇ A_ n, ─ (v_ n) $_ n) 美元, 使用 $A_ n _ nabla f (x_ n) =2. Id$ 和 $v_ n= A_ n_ n_ listeal_ line_ n_ little_ 1}.\ nnabla f(x_ n_ n_ n_ n_ n_ n_ n_ n_ n_ 美元) 。 在这里, $ ddelta_ ndelta a_ n_ n_ n_ n_ n_ nar_ nar_ an; 和 $ pral_ ral_ ral_ a road road road rod, road a ral mologs a pass a pass liver liver listrations liver 。 liver listrations the list list listrations a lives lix lives lives lax lives lives liver liver lives liver las 。 lix lix lax lix lix 。 。 。 lix 。 = = = = =n =n_ unxxxxxxxx unxxxxxxxx unx unxxxxxxxxx