Nonparametric Simulation Extrapolation for Measurement Error Models

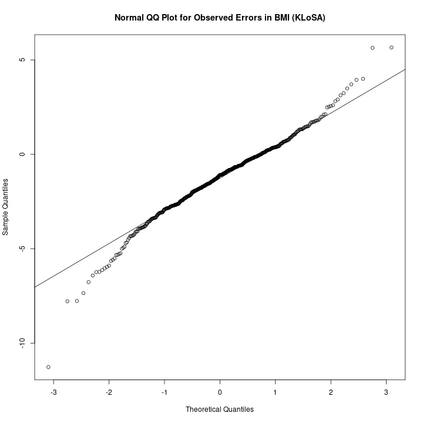
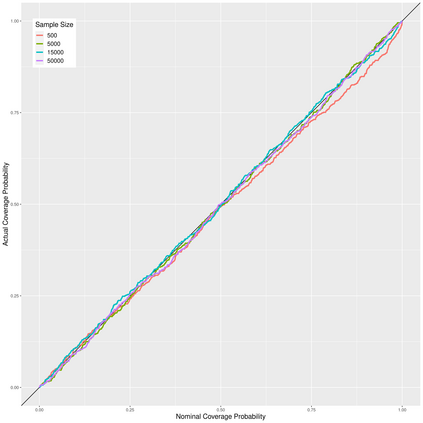
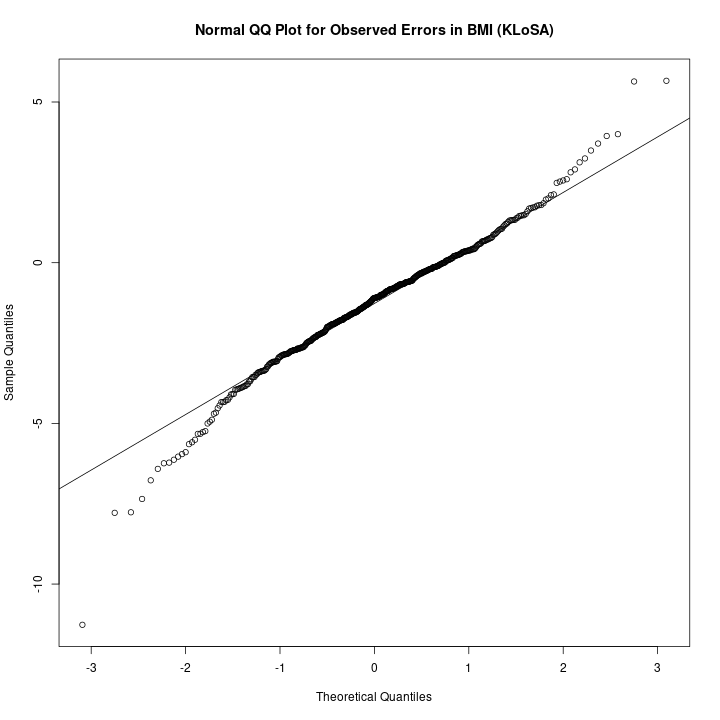
The presence of measurement error is a widespread issue which, when ignored, can render the results of an analysis unreliable. Numerous corrections for the effects of measurement error have been proposed and studied, often under the assumption of a normally distributed, additive measurement error model. One such correction is the simulation extrapolation method, which provides a flexible way of correcting for the effects of error in a wide variety of models, when the errors are approximately normally distributed. However, in many situations observed data are non-symmetric, heavy-tailed, or otherwise highly non-normal. In these settings, correction techniques relying on the assumption of normality are undesirable. We propose an extension to the simulation extrapolation method which is nonparametric in the sense that no specific distributional assumptions are required on the error terms. The technique is implemented when either validation data or replicate measurements are available, and it shares the general structure of the standard simulation extrapolation procedure, making it immediately accessible for those familiar with this technique.