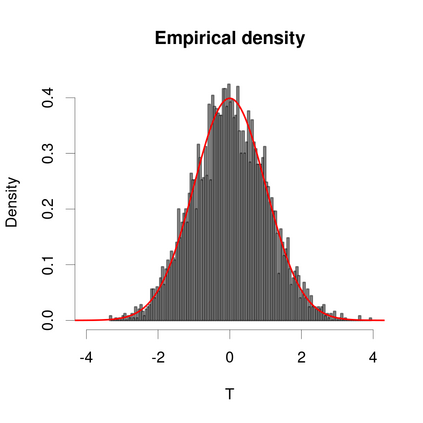
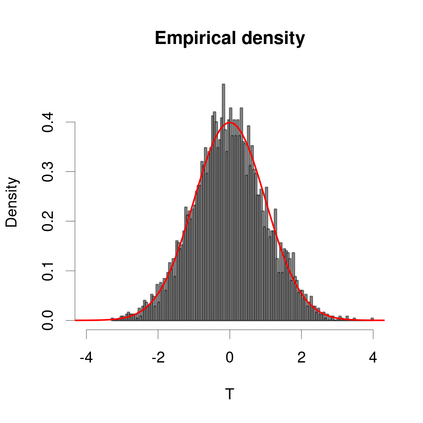
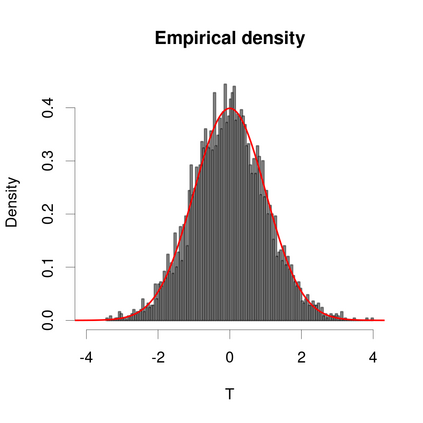
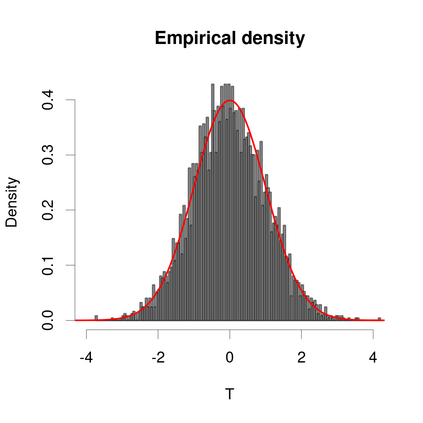
This paper focuses on the separable covariance matrix when the dimension $p$ and the sample size $n$ grow to infinity but the ratio $p/n$ tends to zero. The separable sample covariance matrix can be written as $n^{-1}A^{1/2}XBX^\top A^{1/2}$, where $A$ and $B$ correspond to the cross-row and cross-column correlations, respectively. We normalize the separable sample covariance matrix and prove the central limit theorem for corresponding linear spectral statistics, with explicit formulas for the mean and covariance function. We apply the results to testing the correlations of a large number of variables with two common examples, related to spatial-temporal model and matrix-variate model, which are beyond the scenarios considered in existing studies. The asymptotic sizes and powers are studied under mild conditions. The computations of the asymptotic mean and variance are involved under the null hypothesis where $A$ is the identity matrix, with simplified expressions which facilitate to practical usefulness. Extensive numerical studies show that the proposed testing statistic performs sufficiently reliably under both the null and alternative hypothesis, while a conventional competitor fails to control empirical sizes.
翻译:本文侧重于当维度为美元和样本规模为美元到无限值时的可分离共变矩阵, 当维度为美元和样本大小为美元,但比例为美元/美元时, 则标度为零时, 可分离的样本共变矩阵可以写成美元($ ⁇ -1}A ⁇ 1/2}XUX* ⁇ top A ⁇ 1/2}美元), 美元和美元B$分别对应跨行和交叉列的相互关系。 我们将分离的样本互换矩阵标准化, 并证明对应的线性光谱统计的核心限值, 并配有平均和共变异功能的明确公式。 我们应用结果测试大量变量的相关性, 有两个共同的例子, 与空间时空模型和矩阵变异模型有关, 超出现有研究中考虑的假设。 对无源大小和权力的研究在温和的条件下进行。 在无效假设下, 对无源平均值和差异进行计算, 其中, $A$是身份矩阵, 以及简化的表达方式, 以便于实际使用。 广泛的数字研究显示, 在可靠的假设下, 进行无源和可靠地分析时, 测试, 将进行无源的统计测试。