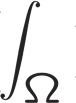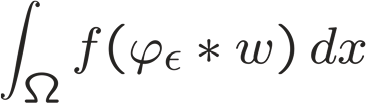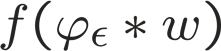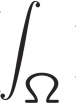We compare the accuracy, convergence rate and computational cost of eigenerosion (EE) and phase-field (PF) methods. For purposes of comparison, we specifically consider the standard test case of a center-crack panel loaded in biaxial tension and assess the convergence of the energy error as the length scale parameter and mesh size tend to zero simultaneously. The panel is discretized by means of a regular mesh consisting of standard bilinear or Q1 elements. The exact stresses from the known analytical linear elastic solution are applied to the boundary. All element integrals over the interior and the boundary of the domain are evaluated exactly using the symbolic computation program Mathematica. When the EE inelastic energy is enhanced by means of Richardson extrapolation, EE is found to converge at twice the rate of PF and to exhibit much better accuracy. In addition, EE affords a one-order-of-magnitude computational speed-up over PF.
翻译:为了进行比较,我们特别考虑在两轴张力下装入的中裂缝面板的标准试验案例,并同时评估能源误差的趋同情况,因为长度表参数和网状尺寸往往为零。该面板通过由标准双线或Q1元素组成的常规网格分解。已知分析线性弹性溶液的精确压力适用于边界。对内和域边界的所有元件都精确地使用数学模拟计算程序进行评估。当EE无弹性能量通过理查森外推法手段增强时,EE被发现以PF速度两倍的速度趋同,而且显示的准确性要大得多。此外,E为PF提供了一阶的放大计算速度。