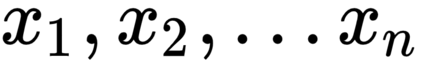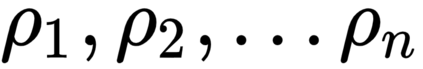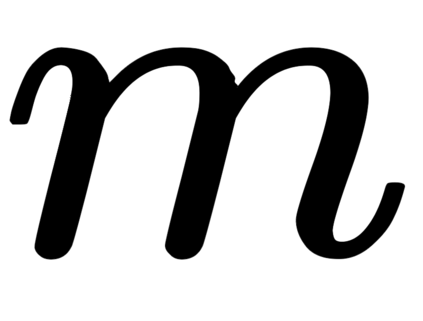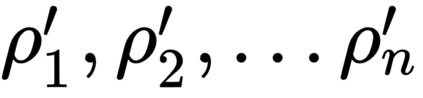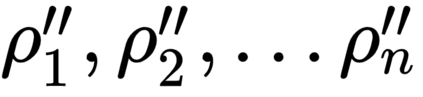The generalized amplitude damping channel (GADC) is considered an important model for quantum communications, especially over optical networks. We make two salient contributions in this paper apropos of this channel. First, we consider a symmetric GAD channel characterized by the parameter $n=1/2,$ and derive its exact classical capacity, by constructing a specific induced classical channel. We show that the Holevo quantity for the GAD channel equals the Shannon capacity of the induced binary symmetric channel, establishing at once the capacity result and that the GAD channel capacity can be achieved without the use of entanglement at the encoder or joint measurements at the decoder. Second, motivated by the inevitable buffering of qubits in quantum networks, we consider a generalized amplitude damping \emph{queue-channel} -- that is, a setting where qubits suffer a waiting time dependent GAD noise as they wait in a buffer to be transmitted. This GAD queue channel is characterized by non-i.i.d. noise due to correlated waiting times of consecutive qubits. We exploit a conditional independence property in conjunction with additivity of the channel model, to obtain a capacity expression for the GAD queue channel in terms of the stationary waiting time in the queue. Our results provide useful insights towards designing practical quantum communication networks, and highlight the need to explicitly model the impact of buffering.
翻译:通用的振幅阻隔频道(GADC)被认为是量子通信的重要模式, 特别是在光学网络上。 我们在本文件中做出两个显著贡献, 以这个频道为方案。 首先, 我们考虑以参数$=1/2为特点的对称 GAD 频道, 并通过建造一个特定的导引古典频道, 得出其精确的古典能力。 我们显示, Holevo 频道的量相当于 引导的二进制对称频道的香农能力, 一次确定能力结果, 并且GAD 频道的容量可以实现, 而不使用 缓冲器的缠绕或对解色器的联合测量。 第二, 我们考虑一个由量网络中QOD 不可避免的缓冲驱动的对称 GAD 频道。 我们利用一个通用的斜度, 在缓冲时等待GAD 频道的等待时间噪音, 这个缓冲器将立即建立起来, 这个 GAD 排队列的排队列的排队列 以不使用 i. d. d. 由于连续的缓冲时间等待模型等待时间 而在缓冲 的缓冲状态上, 我们的阵列队列的队列的队列的队列的队列的队列的队列 将获得了方向 。