Constructing the Field of Values of Decomposable and General Matrices Using the ZNN Based Path Following Method

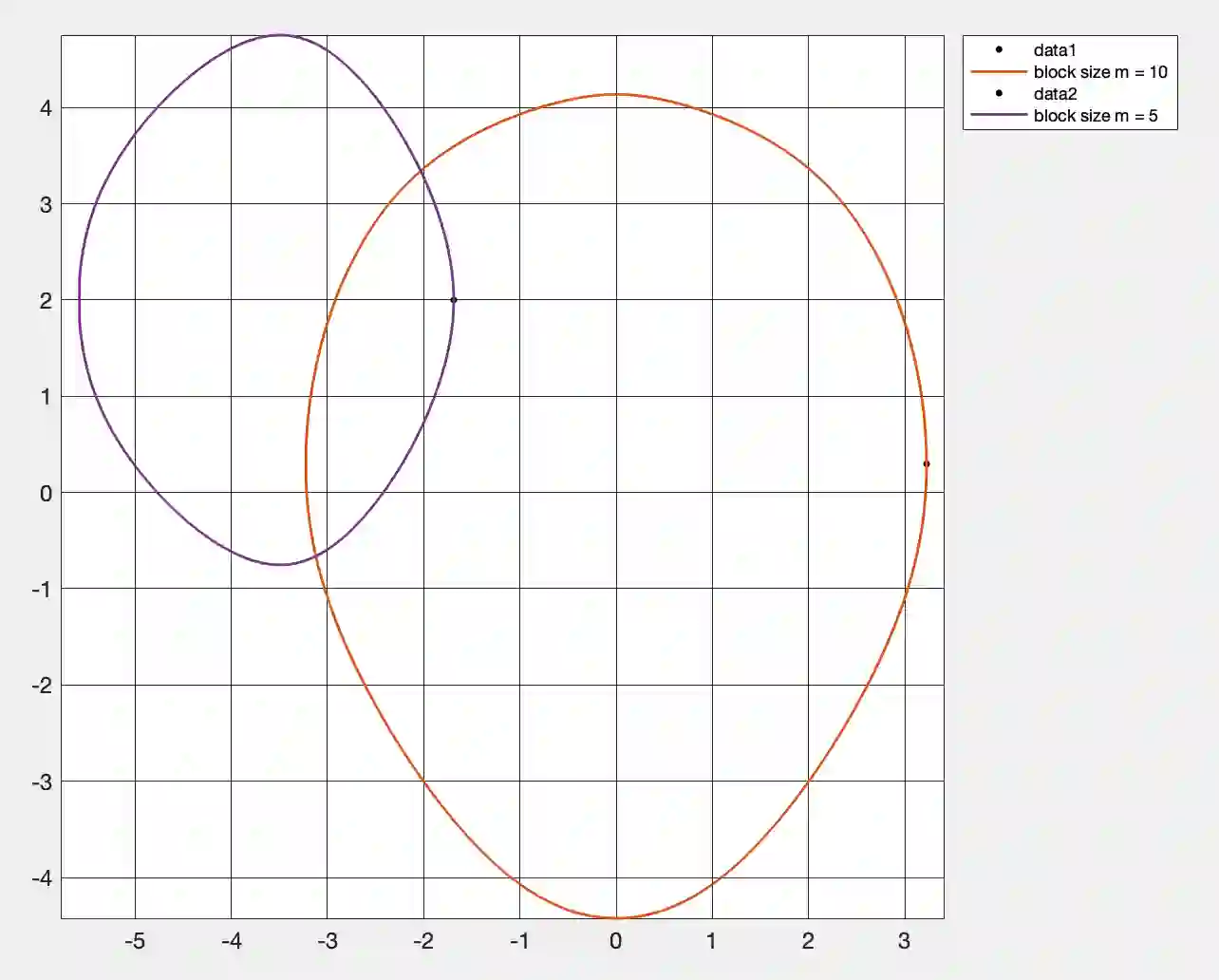
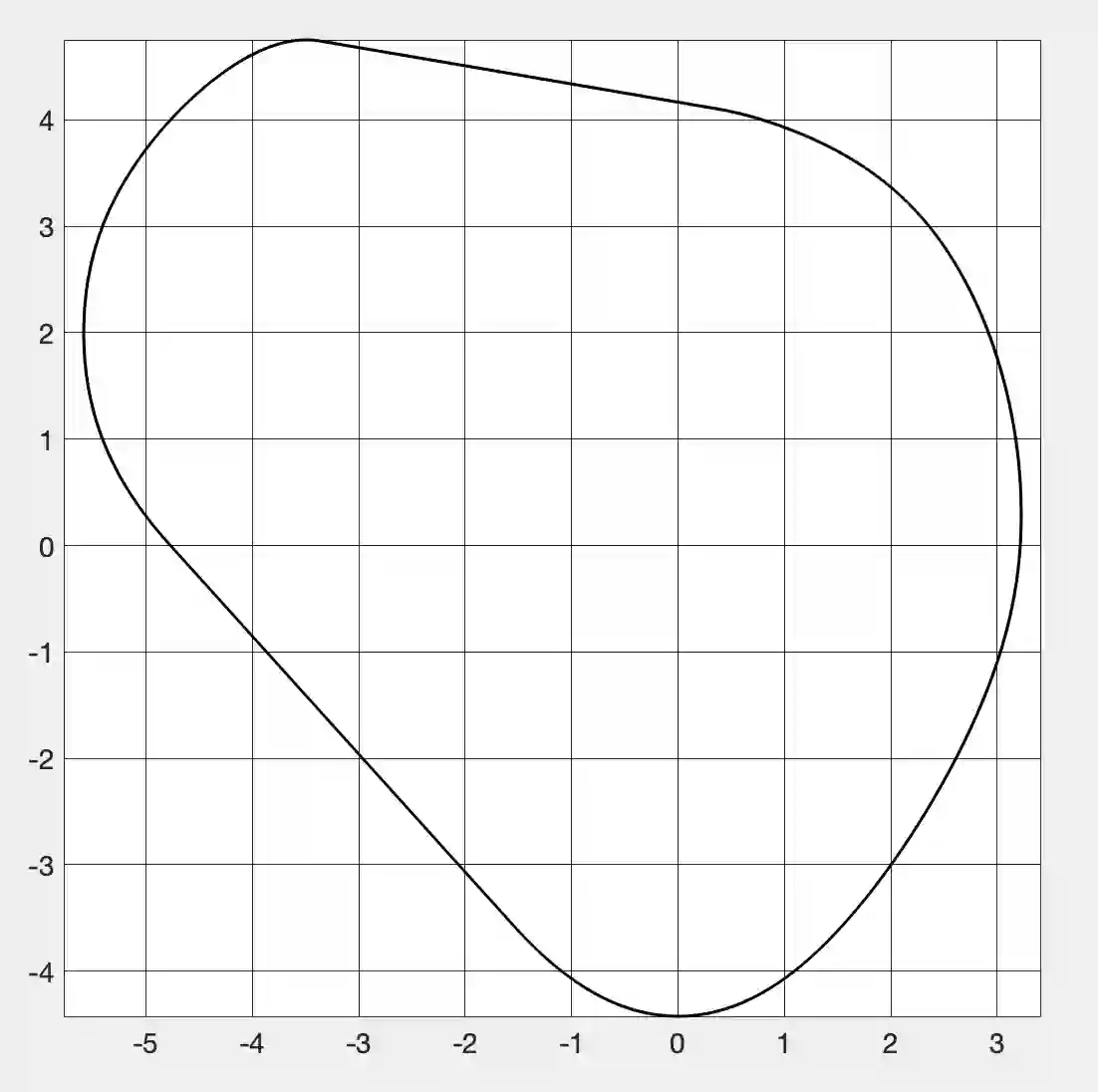
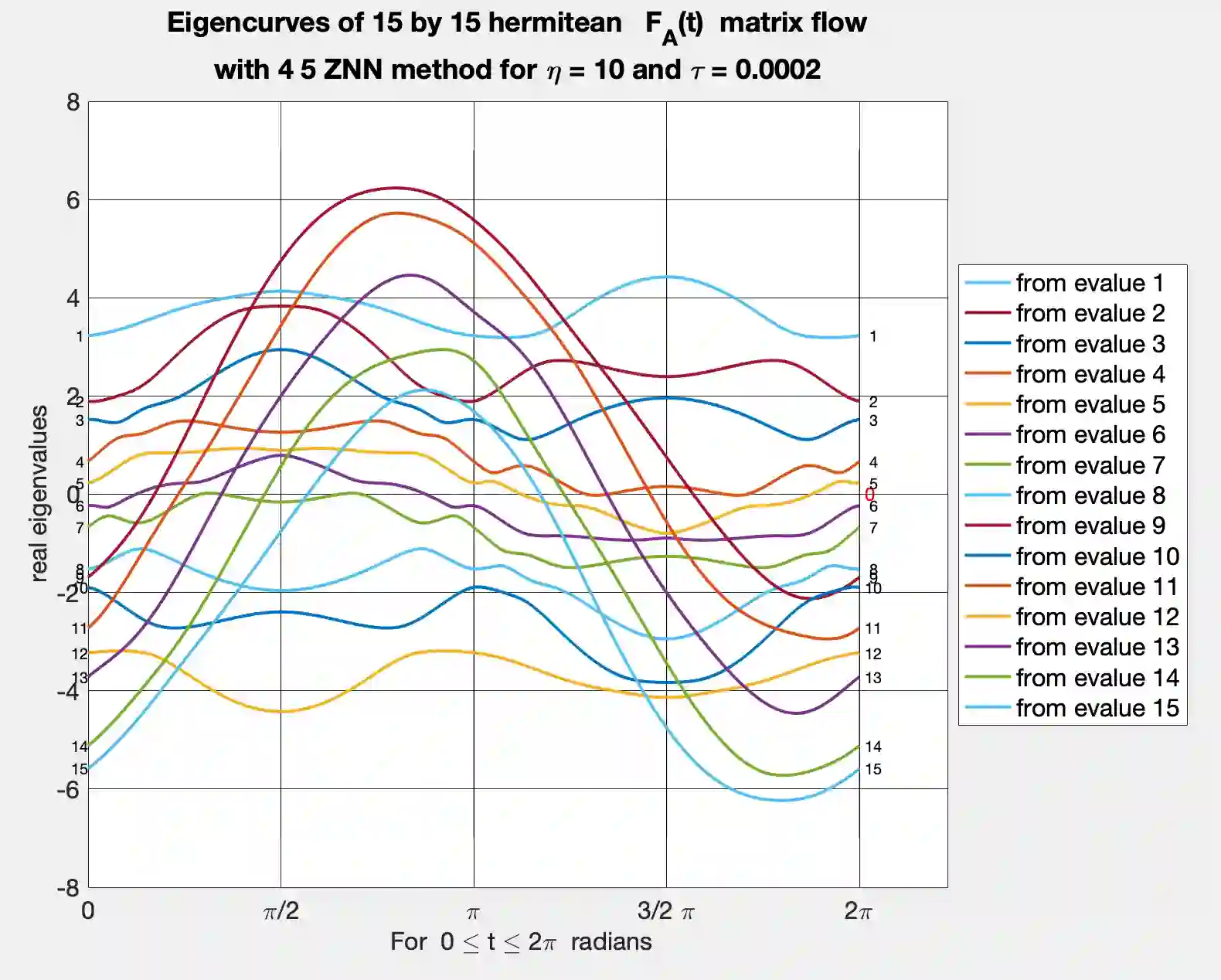
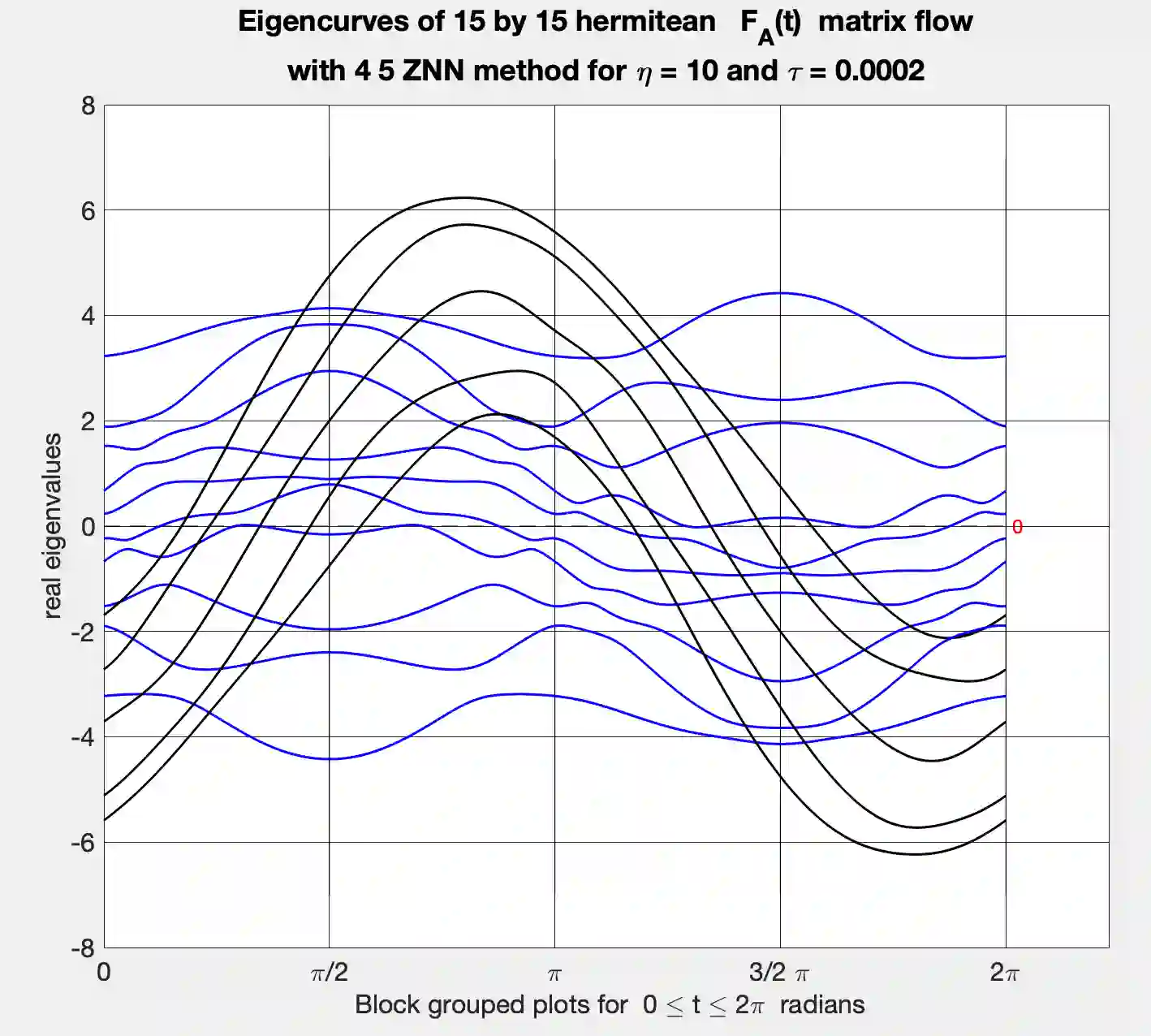
This paper describes and develops a fast and accurate path following algorithm that computes the field of values boundary curve for every conceivable complex or real square matrix $A$. It relies on a matrix flow decomposition method that finds a proper block-diagonal flow representation for the associated hermitean matrix flow ${\cal F}_A(t) = \cos(t) H + \sin(t) K$. Here ${\cal F}_A(t)$ is a 1-parameter-varying linear combination of the real and skew part matrices $H = (A+A^*)/2$ and $K = (A-A^*)/(2i)$ of $A$. For decomposing flows ${\cal F}_A(t)$, the algorithm decomposes a given dense general matrix $A$ unitarily into block-diagonal form $U^*AU = \text { diag} (A_j)$ with $j > 1$ diagonal blocks $A_j$ whose individual sizes add up to the size of $A$. It then computes the field of values boundaries separately for each diagonal block $A_j$ using the path following ZNN eigenvalue method. The convex hull of all sub-fields of values boundary points then determines the field of values boundary curve correctly for decomposing and non-decomposing matrices $A$. The algorithm removes standard restrictions for path following FoV methods that generally cannot deal with decomposing matrices $A$ due to possible eigencurve crossings of ${\cal F}_A(t)$. Tests and numerical comparisons are included. Our ZNN based method is coded for sequential and parallel computations and both versions run very accurately and very fast when compared with Johnson's Francis QR eigenvalue and Bendixon rectangle based method that computes complete eigenanalyses of ${\cal F}_A(t_k)$ for every chosen $t_k \in {[} 0,2\pi{]}$ more slowly.