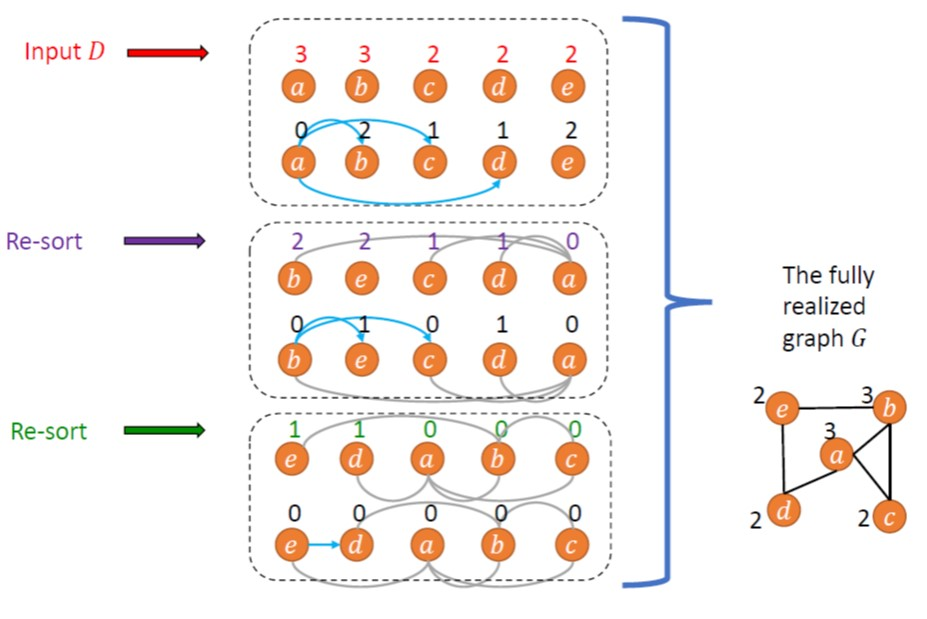
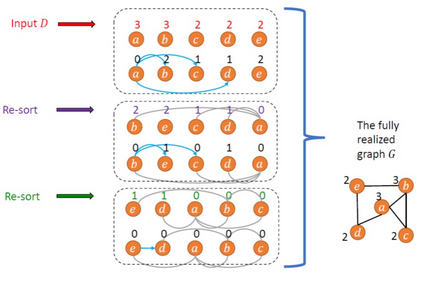
We study graph realization problems from a distributed perspective and we study it in the node capacitated clique (NCC) model of distributed computing, recently introduced for representing peer-to-peer networks. We focus on two central variants, degree-sequence realization and minimum threshold-connectivity realization both of which result in overlay network realizations. Overlay network realizations can be either explicit or implicit. Explicit realizations require both endpoints of any edge in the realized graph to be aware of the edge. In implicit realizations, on the other hand, at least one endpoint of each edge of the realized graph needs to be aware of the edge. The main realization algorithms we present are the following. 1. An $\tilde{O}(\min\{\sqrt{m},\Delta\})$ time algorithm for implicit realization of a degree sequence. Here, $\Delta = \max_v d(v)$ is the maximum degree and $m = (1/2) \sum_v d(v)$ is the number of edges in the final realization. An $\tilde{O}(\Delta)$ time algorithm for an explicit realization of a degree sequence. We first compute an implicit realization and then transform it into an explicit one in $\tilde{O}(\Delta)$ additional rounds. 2. An $\tilde{O}(\Delta)$ time algorithm for the threshold connectivity problem that obtains an explicit solution and an improved $\tilde{O}(1)$ algorithm for implicit realization when all nodes know each other's IDs. These algorithms are 2-approximations w.r.t. the number of edges. We complement our upper bounds with lower bounds to show that the above algorithms are tight up to factors of $\log n$. Additionally, we provide algorithms for realizing trees and an $\tilde{O}(1)$ round algorithm for approximate degree sequence realization.
翻译:我们从分布式角度来分析实现问题, 我们在分布式计算节点{ 电解算 (NCC) 模型中研究这一问题, 最近为代表同侪对同侪网络引入的分布式计算。 我们侧重于两个中心变体, 度序列的实现和最小端点- 连接度的实现, 导致覆盖网络的实现。 重叠网络的实现可以是明确或隐含的。 显而易见的实现需要实现图中任何边缘的终点, 以了解边缘。 另一方面, 在隐含的实现中, 至少有一个已实现的图边缘端点需要了解边缘 。 我们介绍的主要实现算法如下。 1 $\ tilde{ 级序列的实现和最小端点。 $\\ Qelqrt{ m} 。 $Delta=\ dv 以上的任何端点是最大度和 美元 ==== == = === == == ==== == ===== === = ===== 最低端端端点, 实现最后实现一个直值。