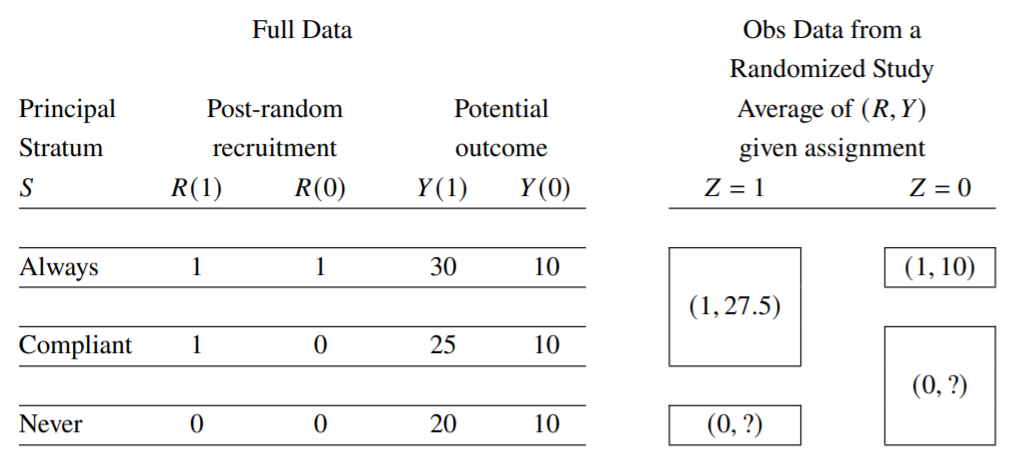
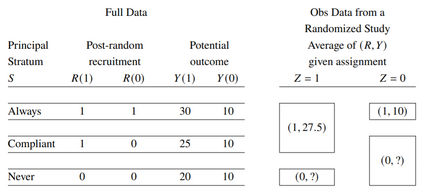
In cluster randomized trials, patients are typically recruited after clusters are randomized, and the recruiters and patients may not be blinded to the assignment. This often leads to differential recruitment and consequently systematic differences in baseline characteristics of the recruited patients between intervention and control arms, inducing post-randomization selection bias. We rigorously define causal estimands in the presence of selection bias. We elucidate the conditions under which standard covariate adjustment methods can validly estimate these estimands. We further discuss the additional data and assumptions necessary for estimating causal effects when such conditions are not met. Adopting the principal stratification framework in causal inference, we clarify there are two average treatment effect (ATE) estimands in cluster randomized trials: one for the overall population and one for the recruited population. We derive the analytical formula of the two estimands in terms of principal-stratum-specific causal effects. Using simulation studies, we assess the empirical performance of the multivariable regression adjustment method under different data generating processes leading to selection bias. When treatment effects are heterogeneous across principal strata, the ATE on the overall population generally differs from the ATE on the recruited population. An intention-to-treat analysis of the recruited sample leads to biased estimates of both ATEs. In the presence of post-randomization selection and without additional data on the non-recruited subjects, the ATE on the recruited population is estimable only when the treatment effects are homogenous between principal strata, and the ATE on the overall population is generally not estimable. The extent to which covariate adjustment can remove selection bias depends on the degree of effect heterogeneity across principal strata.
翻译:在集束随机试验中,典型的病人是在随机随机分组后招聘的,而招聘者和病人可能不会盲目于分派任务,这往往导致不同的征聘,从而导致在干预和控制武器之间征聘病人的基准特征上出现系统的差异,从而导致随机选择后的选择偏差。我们严格界定因果估计值,同时存在选择偏差。我们阐明了标准共变调整方法能够有效估计这些估计值的条件。我们进一步讨论了在不满足此类条件时估算因果关系所必需的额外数据和假设。在采用因果推断的主要分级框架时,我们澄清了在集束随机测试中,所征聘的病人的基准特征有两种平均的治疗效果(ATE):一个是整个人口,一个是被随机挑选的病人;我们得出两个估计值的分析公式,即本数特定因果影响。我们利用模拟研究,评估可变回归调整方法在产生选择偏差的不同数据过程中的经验性表现。当主要阶层之间出现差异时,在总体人口不因果程度上,我们澄清了总体人口非分类的治疗效果(ATE)在分组随机测试中,一般而言,在征聘人员选择主要选择对象的性别等级上,在征聘对象之间,在征聘后,可变数分析可变数之间,可变数分析可测算。