Accelerated First Order Methods for Variational Imaging

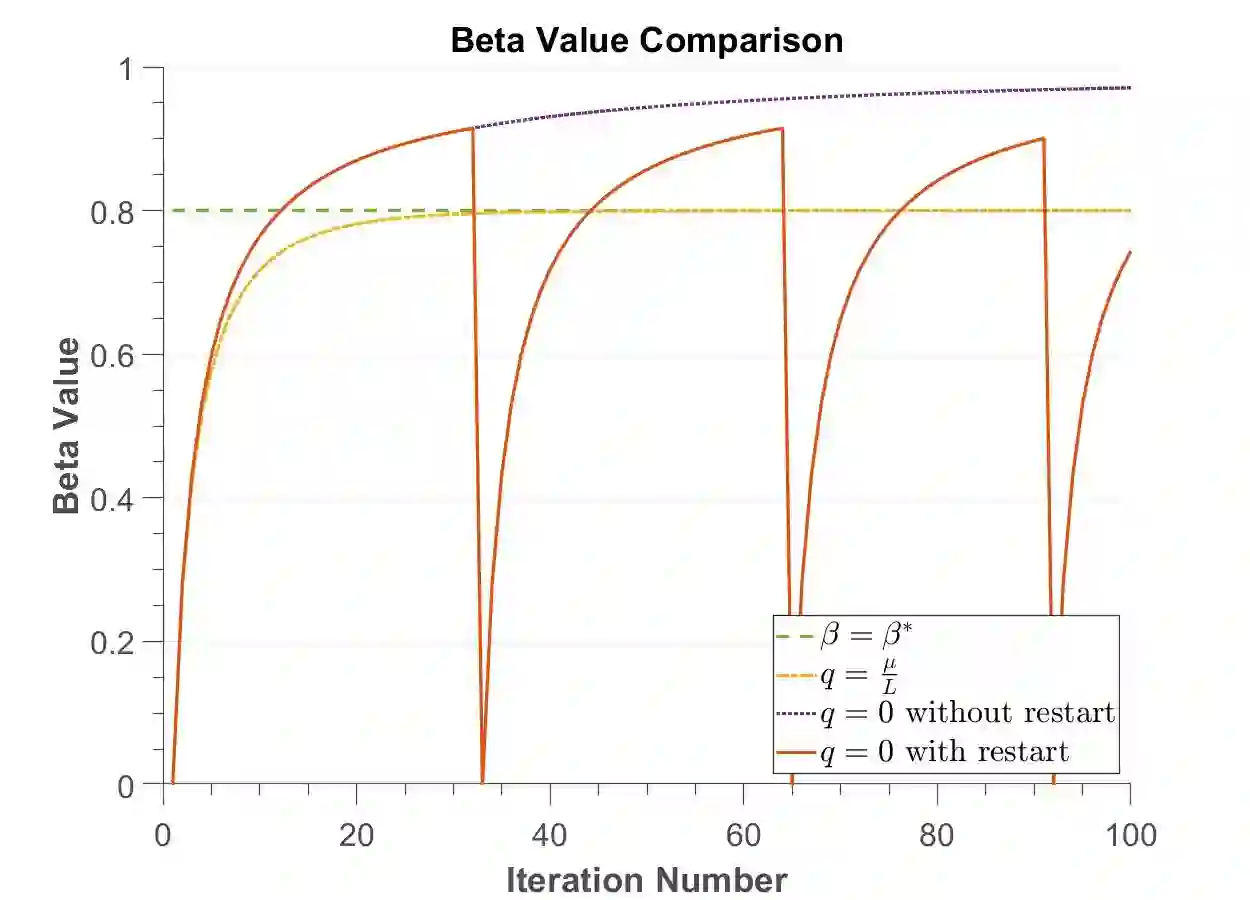
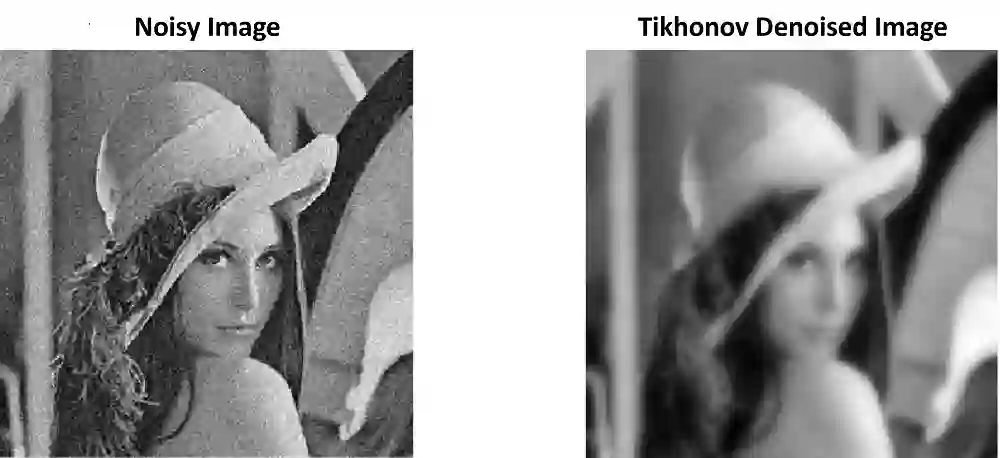
In this thesis, we offer a thorough investigation of different regularisation terms used in variational imaging problems, together with detailed optimisation processes of these problems. We begin by studying smooth problems and partially non-smooth problems in the form of Tikhonov denoising and Total Variation (TV) denoising, respectively. For Tikhonov denoising, we study an accelerated gradient method with adaptive restart, which shows a very rapid convergence rate. However, it is not straightforward to apply this fast algorithm to TV denoising, due to the non-smoothness of its built-in regularisation. To tackle this issue, we propose to utilise duality to convert such a non-smooth problem into a smooth one so that the accelerated gradient method with restart applies naturally. However, we notice that both Tikhonov and TV regularisations have drawbacks, in the form of blurred image edges and staircase artefacts, respectively. To overcome these drawbacks, we propose a novel adaption to Total Generalised Variation (TGV) regularisation called Total Smooth Variation (TSV), which retains edges and meanwhile does not produce results which contain staircase artefacts. To optimise TSV effectively, we then propose the Accelerated Proximal Gradient Algorithm (APGA) which also utilises adaptive restart techniques. Compared to existing state-of-the-art regularisations (e.g. TV), TSV is shown to obtain more effective results on denoising problems as well as advanced imaging applications such as magnetic resonance imaging (MRI) reconstruction and optical flow. TSV removes the staircase artefacts observed when using TV regularisation, but has the added advantage over TGV that it can be efficiently optimised using gradient based methods with Nesterov acceleration and adaptive restart. Code is available at https://github.com/Jbartlett6/Accelerated-First-Order-Method-for-Variational-Imaging.