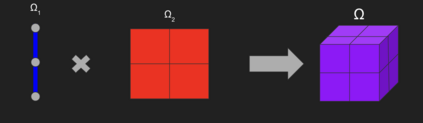
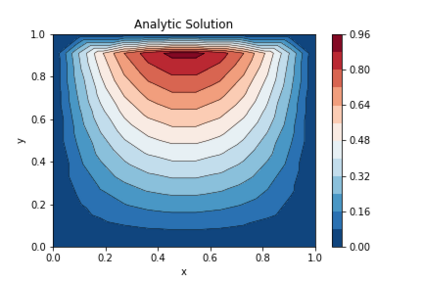
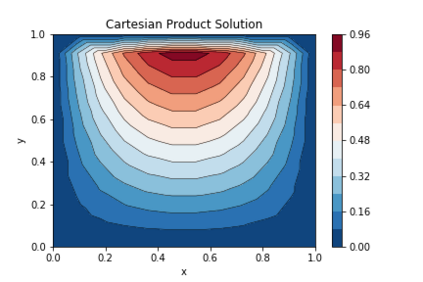
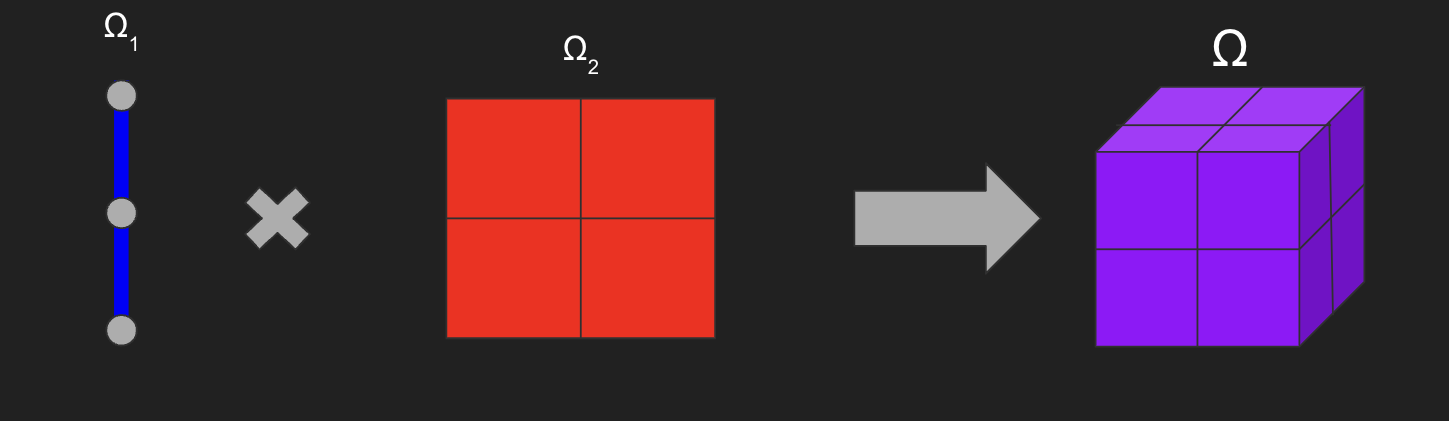
We present a method to extend the finite element library FEniCS to solve problems with domains in dimensions above three by constructing tensor product finite elements. This methodology only requires that the high dimensional domain is structured as a Cartesian product of two lower dimensional subdomains. In this study we consider Dirichlet problems for scalar linear partial differential equations, though the methodology can be extended to non-linear problems. The utilization of tensor product finite elements allows us to construct a global system of linear algebraic equations that only relies on the finite element infrastructure of the lower dimensional subdomains contained in FEniCS. We demonstrate the effectiveness of our methodology in four distinctive test cases. The first test case is a Poisson equation posed in a four dimensional domain which is a Cartesian product of two unit squares solved using the classical Galerkin finite element method. The second test case is the wave equation in space-time, where the computational domain is a Cartesian product of a two dimensional space grid and a one dimensional time interval. In this second case we also employ the Galerkin method. The third test case is an advection dominated advection-diffusion equation where the global domain is a Cartesian product of two one dimensional intervals in which the streamline upwind Petrov-Galerkin method is applied to ensure discrete stability. The final test case uses the Galerkin approach to solve a Poisson problem on a Cartesian product of two intervals with a spatially varying, non-separable diffusivity term. In all cases, a p=1 basis is used and optimal L^2 convergence rates of order h^{p+1} of the errors are achieved with respect to h refinement
翻译:我们提出一个方法来扩大有限元素库 FENICS, 以通过构建 Exronor 产品限制元素来解决三维以上域的问题。 这个方法仅要求高维域的结构结构化为两个低维子域的卡尔泰斯产物。 在此研究中, 我们考虑Drichlet 的卡路里线线性部分差异方程式问题, 尽管该方法可以扩展至非线性问题。 使用 Extor 产品限制元素使我们能够构建一个全球系统, 线性代数方程式的系统, 仅依赖于FEniCS 所含低维次域次域的有限元素基础设施。 我们用四个不同的测试案例来展示我们的方法的有效性。 第一个测试案例是在四维域域内设置的普瓦森方程式, 这是用古典加勒金元素限值元素法解决的两个单位方程式。 第二个测试案例是空间时的波方程式, 其中计算域域内所有维维度空间网格和一维时隔的卡度变异性方程式。 在第二个案例中, 我们用 Galkintal- durvel 方法使用两个域内测试法 。