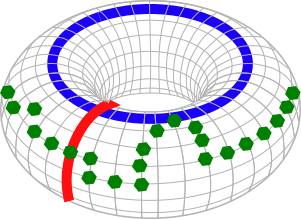
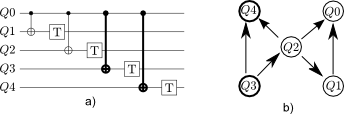
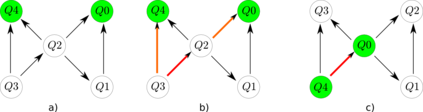
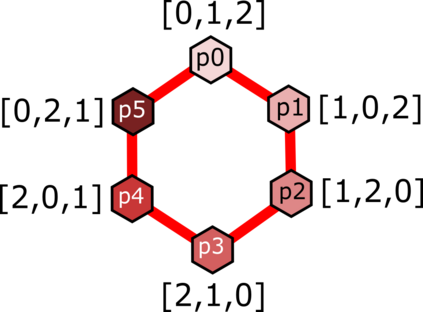
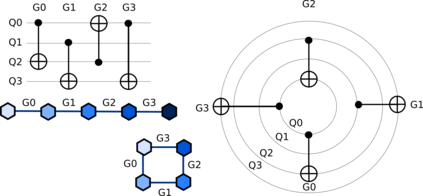
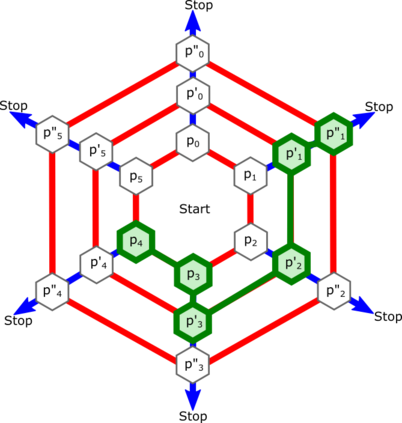
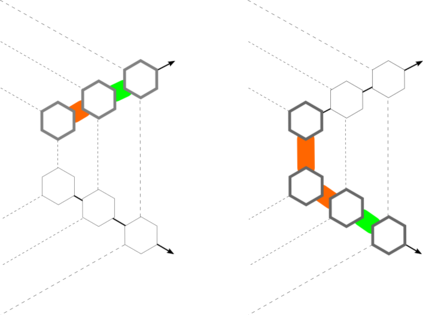
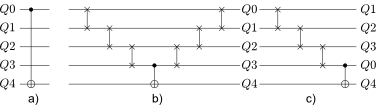
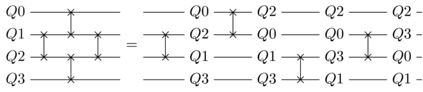
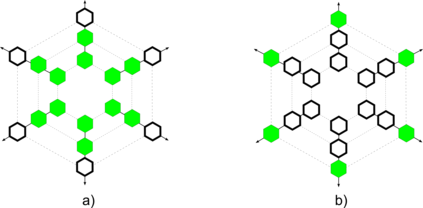
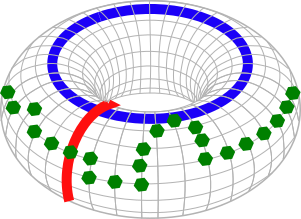
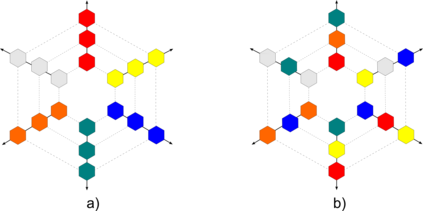Noisy, intermediate-scale quantum (NISQ) computers are expected to execute quantum circuits of up to a few hundred qubits. The circuits have to conform to NISQ architectural constraints regarding qubit allocation and the execution of multi-qubit gates. Quantum circuit compilation (QCC) takes a nonconforming circuit and outputs a compatible circuit. Can classical optimisation methods be used for QCC? Compilation is a known combinatorial problem shown to be solvable by two types of operations: 1) qubit allocation, and 2) gate scheduling. We show informally that the two operations form a discrete ring. The search landscape of QCC is a two dimensional discrete torus where vertices represent configurations of how circuit qubits are allocated to NISQ registers. Torus edges are weighted by the cost of scheduling circuit gates. The novelty of our approach uses the fact that a circuit's gate list is circular: compilation can start from any gate as long as all the gates will be processed, and the compiled circuit has the correct gate order. Our work bridges a theoretical and practical gap between classical circuit design automation and the emerging field of quantum circuit optimisation.
翻译:预计中尺度量子计算机(NISQ)将执行量子电路,最多达几百平方位。电路必须与 NISQ 的建筑限制相符。 量子电路编集( QCC) 采用不兼容的电路和输出相容的电路。 经典优化方法能够用于QCC 吗? 编译是一个已知的组合问题, 由两种类型的操作可以解开:(1) qubit 分配, 和(2) 门排程。 我们非正式地显示, 两种操作形成了一个离散环。 QCC 的搜索场景是两维离心的离心线, 其间脊椎代表着向NISQ 登记册分配电路位的配置。 托鲁斯边缘通过排程门的计价进行加权。 我们的方法的新颖之处是, 电路门的门是圆的: 编译可以从任何门开始, 只要所有门都经过处理, 和编译的电路都有正确的门秩序。 我们的工作桥梁在理论和实践上, 选择电路设计自动化自动化自动化和电路自动化的距离自动化。