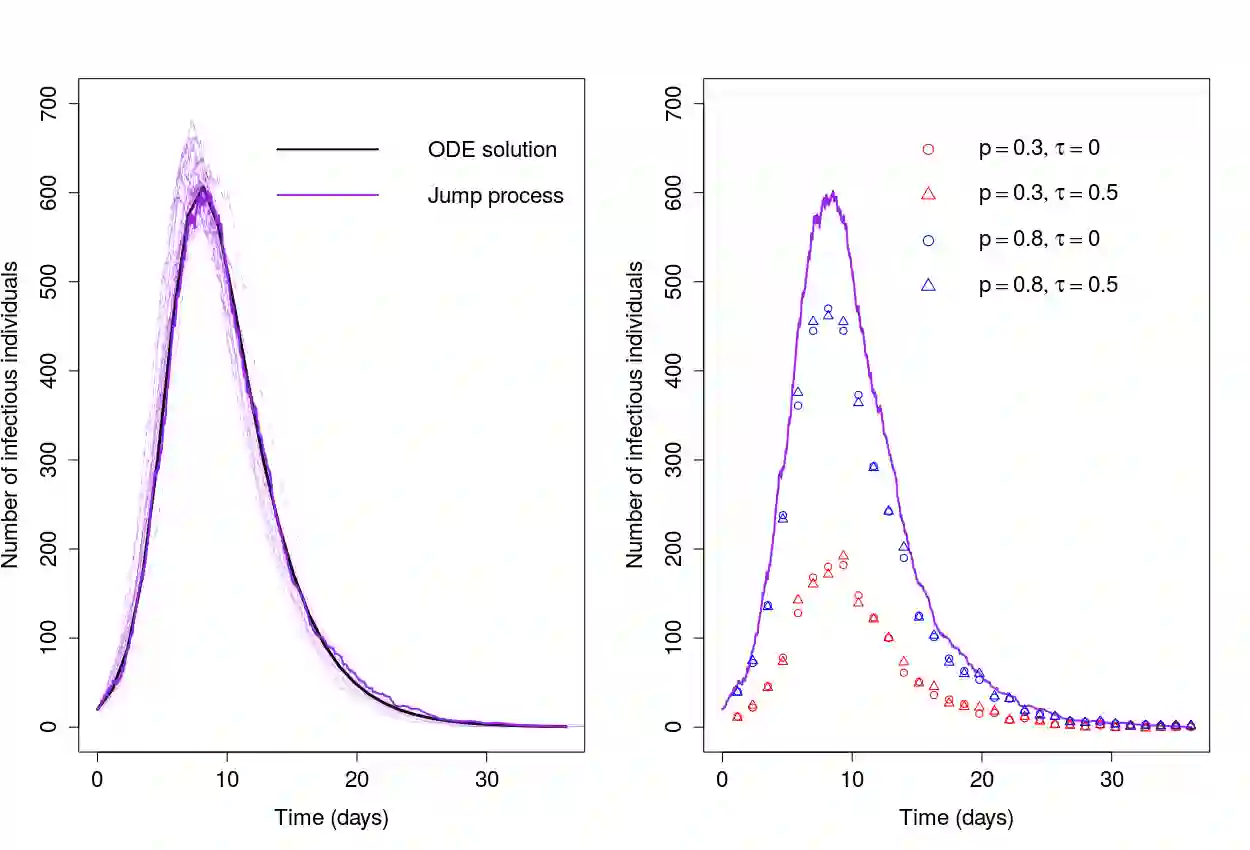
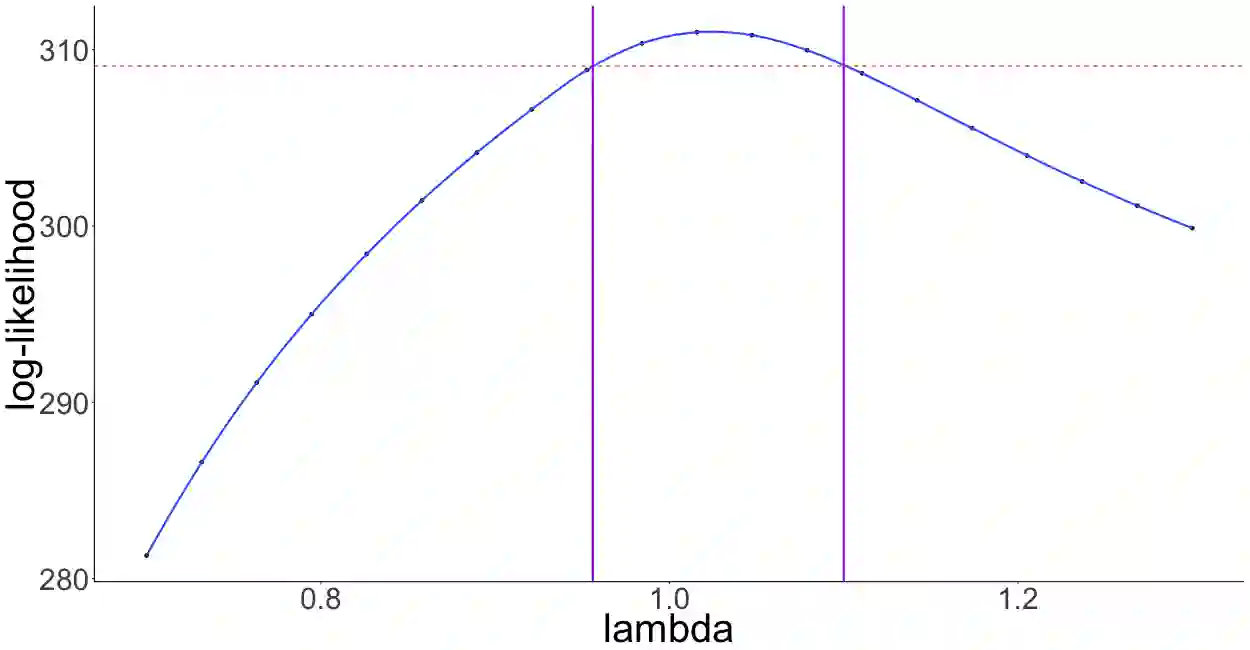
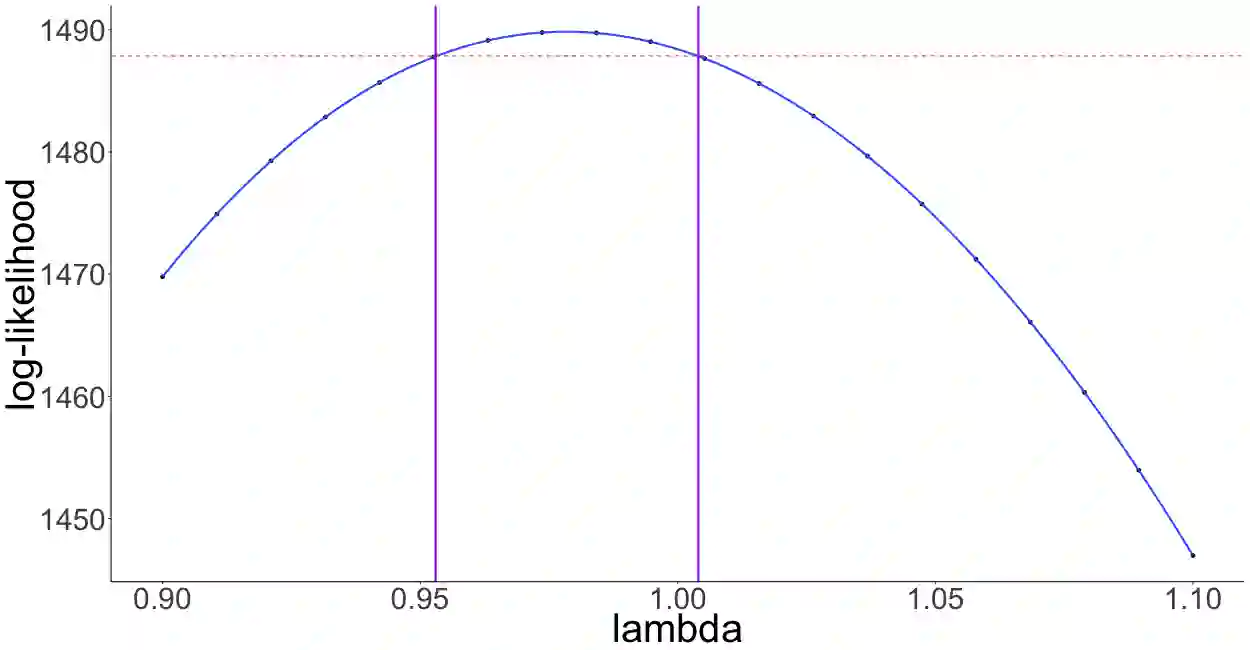
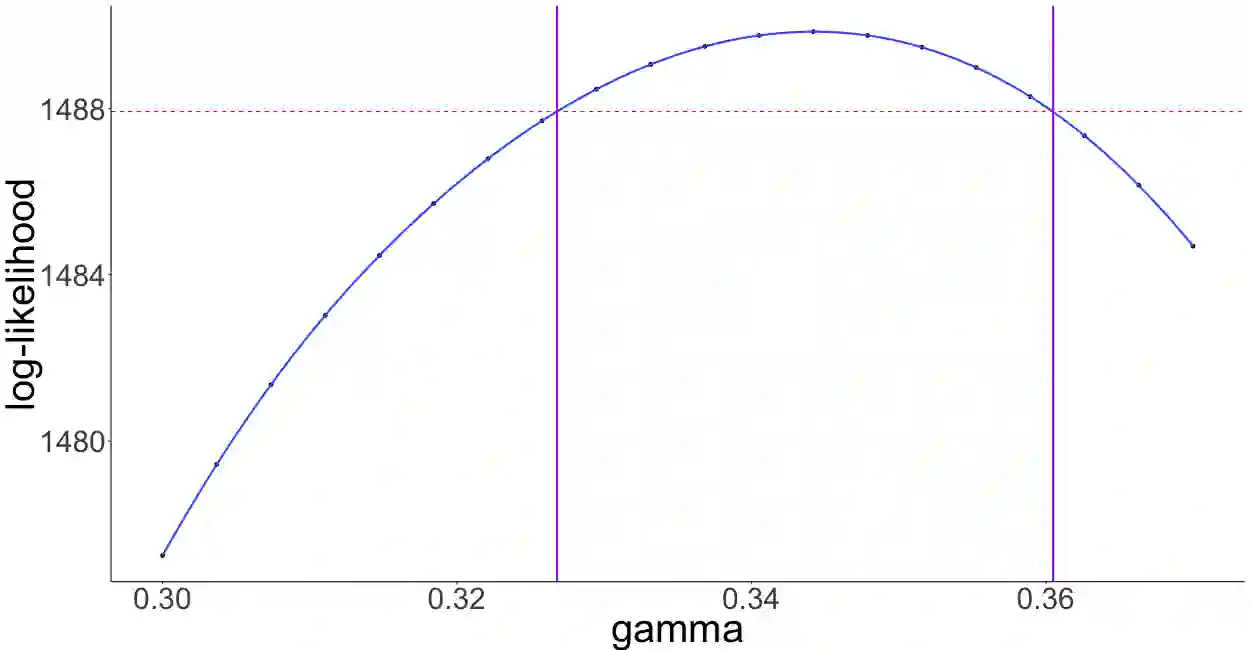
Despite the recent development of methods dealing with partially observed epidemic dynamics (unobserved model coordinates, discrete and noisy outbreak data), limitations remain in practice, mainly related to the quantity of augmented data and calibration of numerous tuning parameters. In particular, as coordinates of dynamic epidemic models are coupled, the presence of unobserved coordinates leads to a statistically difficult problem. The aim is to propose an easy-to-use and general inference method that is able to tackle these issues. First, using the properties of epidemics in large populations, a two-layer model is constructed. Via a diffusion-based approach, a Gaussian approximation of the epidemic density-dependent Markovian jump process is obtained, representing the state model. The observational model, consisting of noisy observations of certain model coordinates, is approximated by Gaussian distributions. Then, an inference method based on an approximate likelihood using Kalman filtering recursion is developed to estimate parameters of both the state and observational models. The performance of estimators of key model parameters is assessed on simulated data of SIR epidemic dynamics for different scenarios with respect to the population size and the number of observations. This performance is compared with that obtained using the well-known maximum iterated filtering method. Finally, the inference method is applied to a real data set on an influenza outbreak in a British boarding school in 1978.
翻译:尽管最近制定了处理部分观察到的流行病动态的方法(未观测模型坐标、离散和噪音爆发数据),但实际中仍存在局限性,主要与扩大数据的数量和许多调试参数的校准有关,特别是,随着动态流行病模型坐标的结合,未观测坐标的出现导致一个统计上的困难问题,目的是提出一种便于使用和一般推论的方法,能够解决这些问题。首先,利用大量人口的流行病特性,构建了两层模型。通过一种基于传播的方法,获得了依赖密度的马尔科维安流行病跳跃过程的Gaussian近似,代表了州模型。观测模型包括对某些模型坐标的密集观测,由高西安分布相近。然后,根据使用卡尔曼过滤性流感循环的大致可能性制定了一种推论方法,以估计国家和观察模型的参数和观察模型的参数。主要模型参数的性能是通过模拟英国SIR流行病动态的模型数据,用于与人口规模和最先进的机率相比,在1978年采用这一方法后期观测中,将采用这一方法。