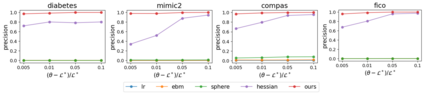
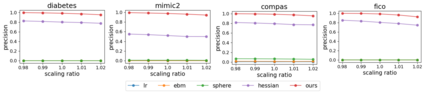
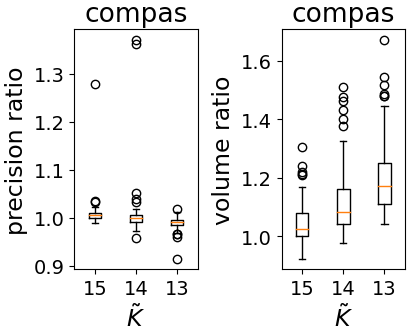
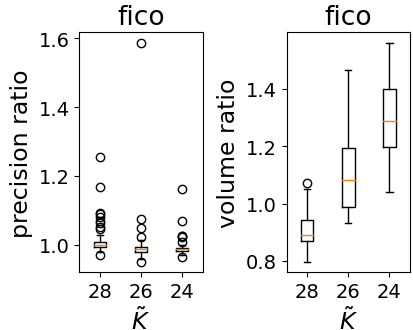
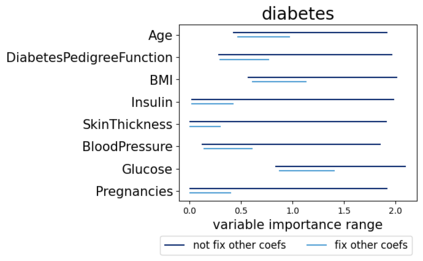
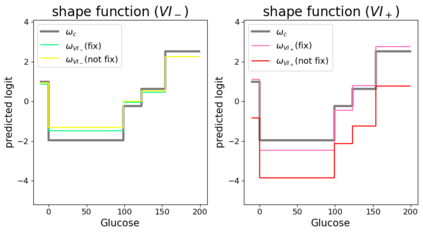
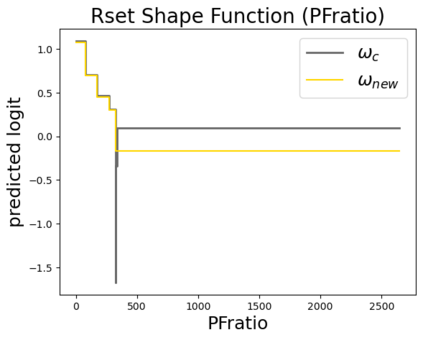
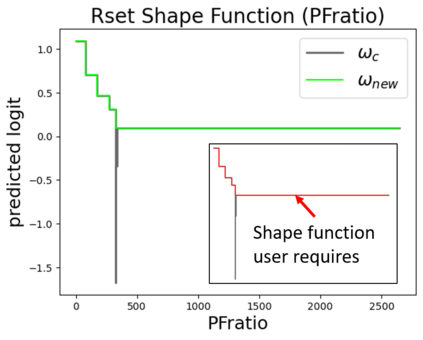
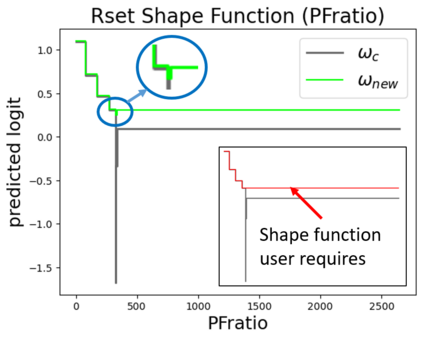
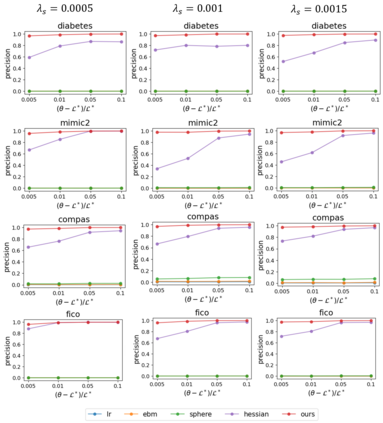
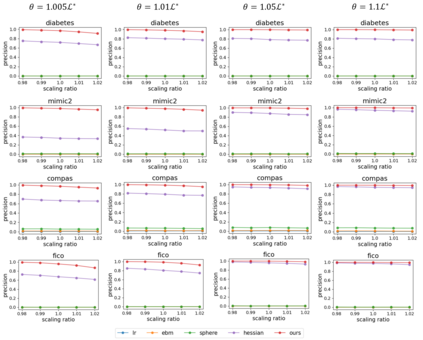
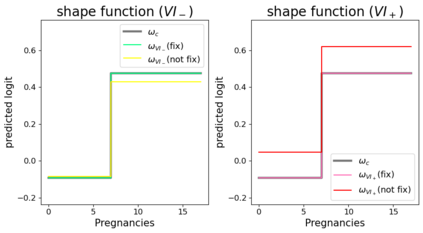
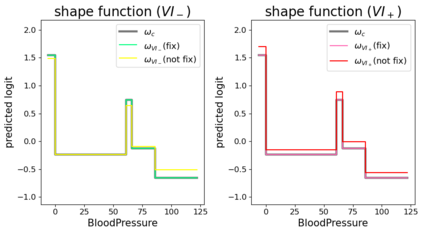
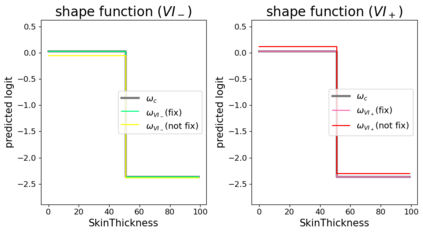
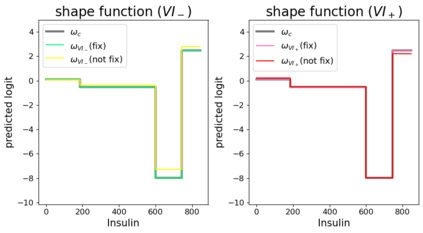
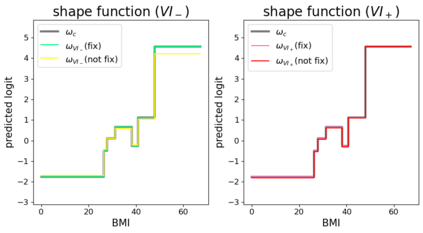
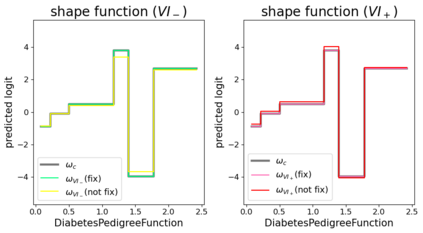
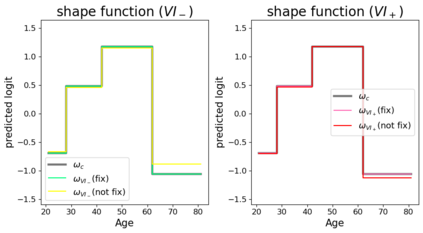
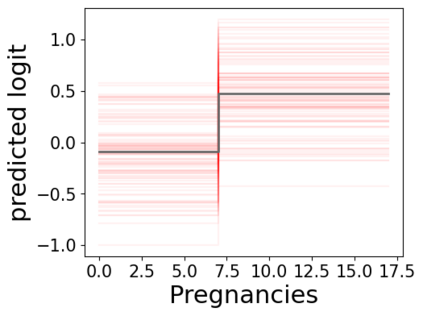
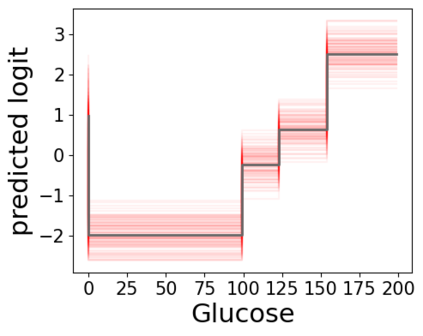
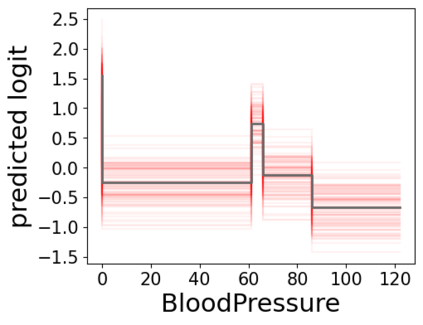
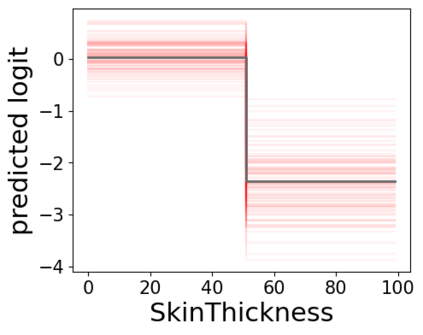
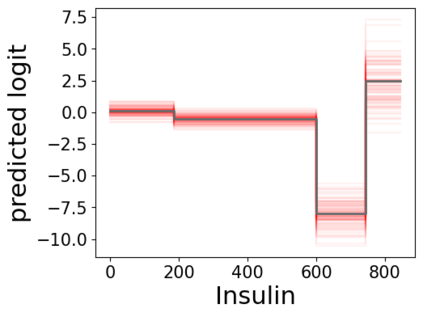
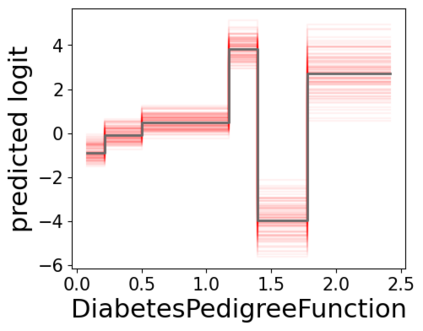
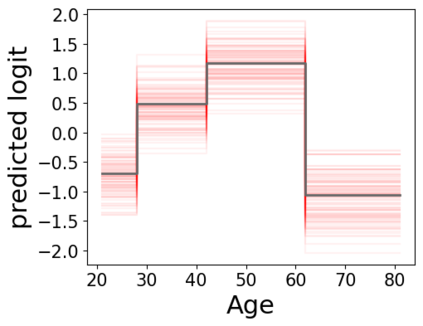
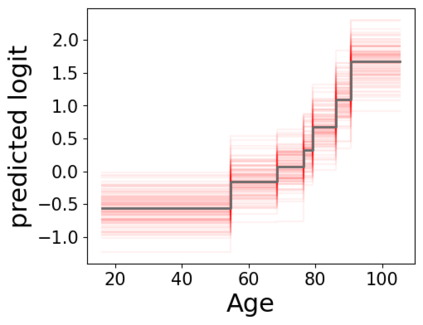
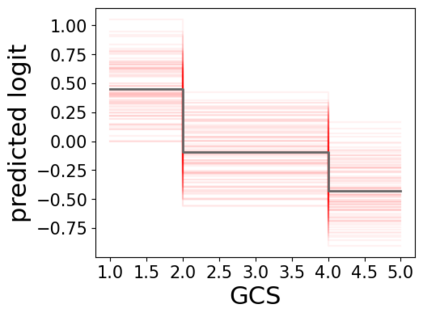
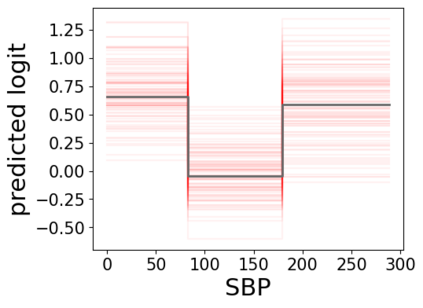
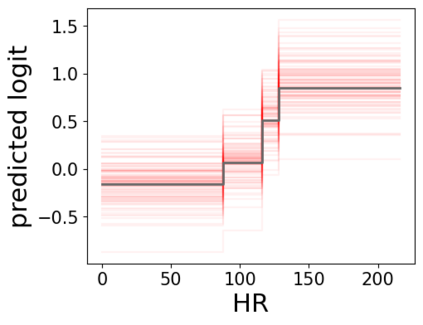
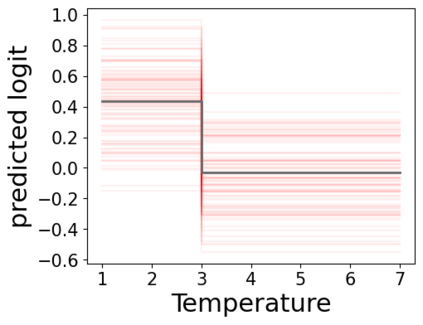
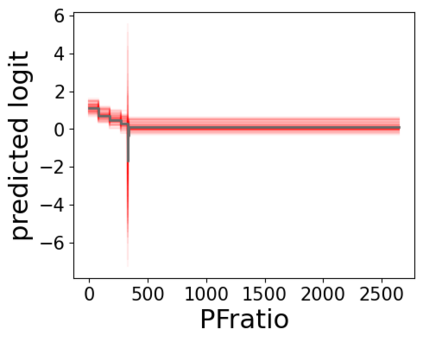
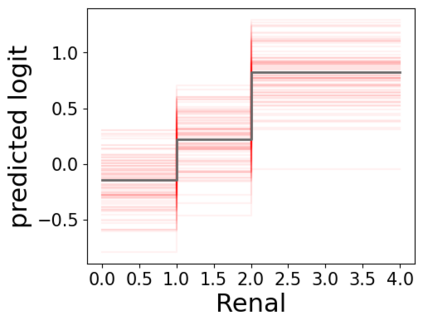
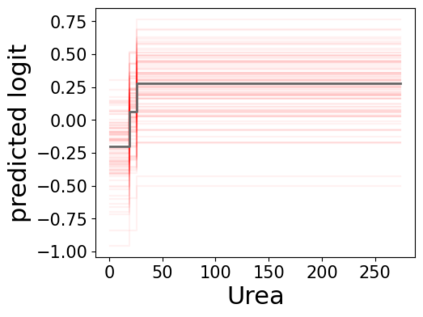
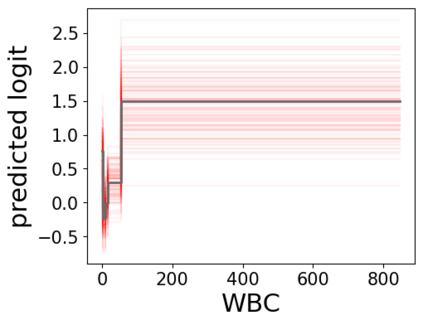
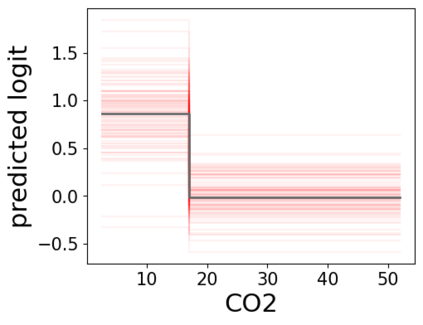
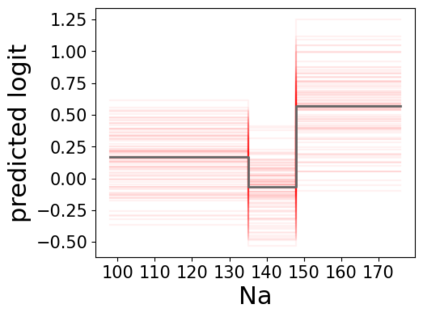
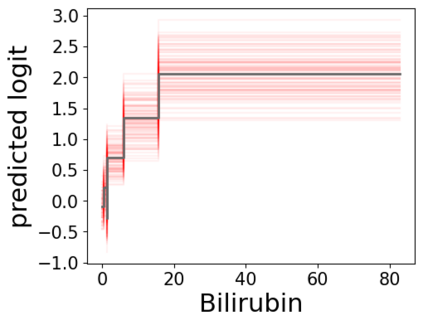
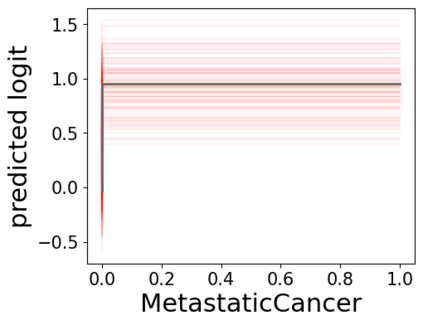
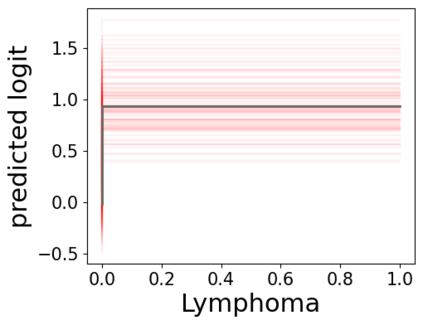
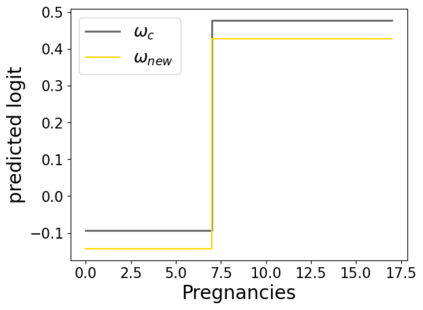
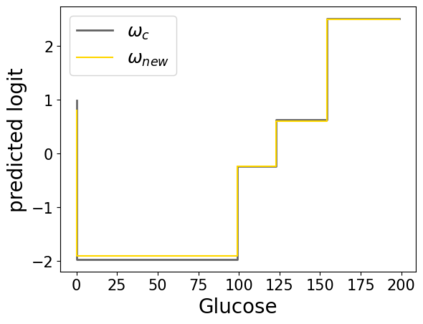
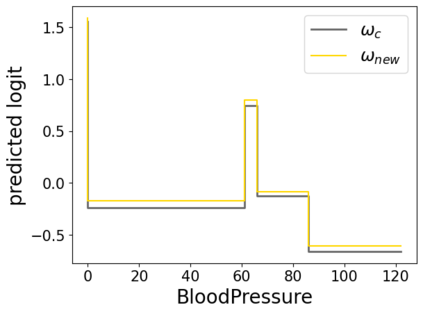
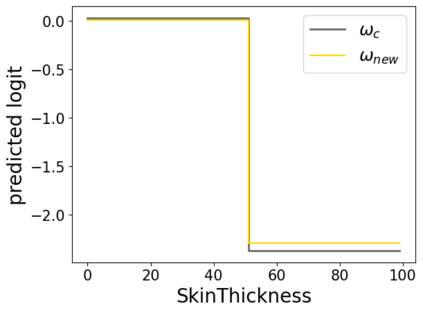
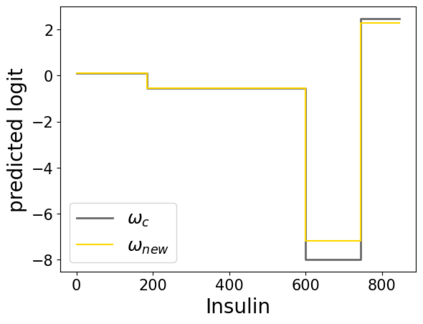
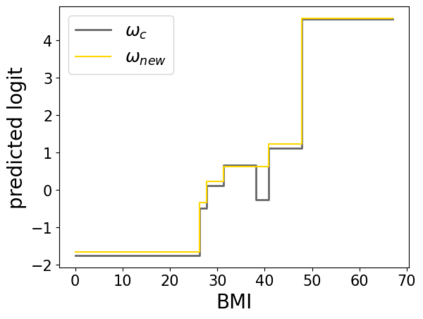
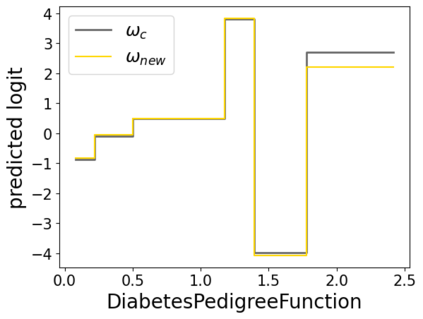
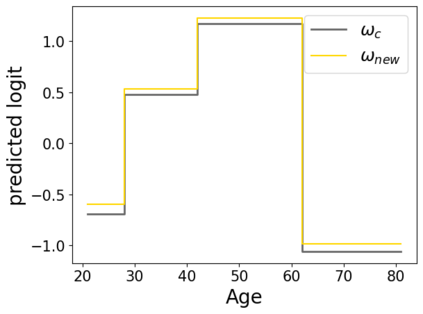
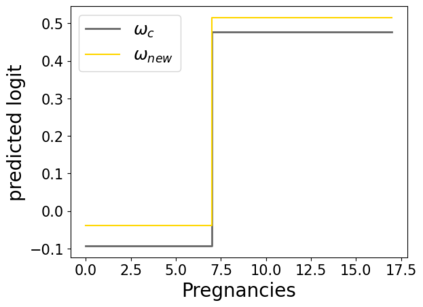
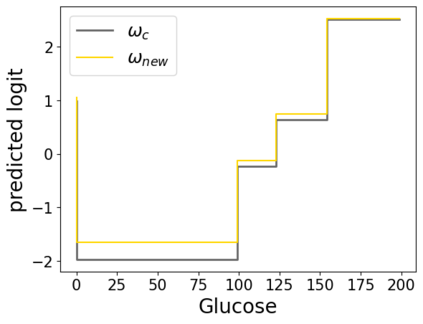
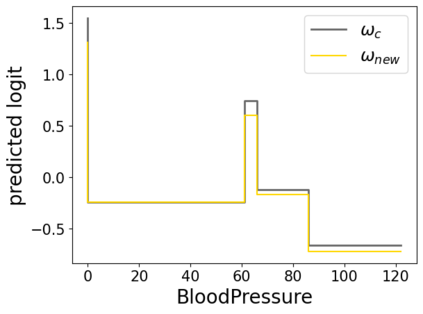
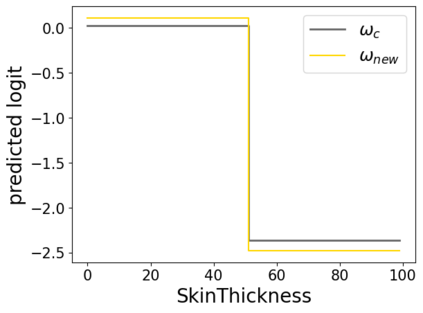
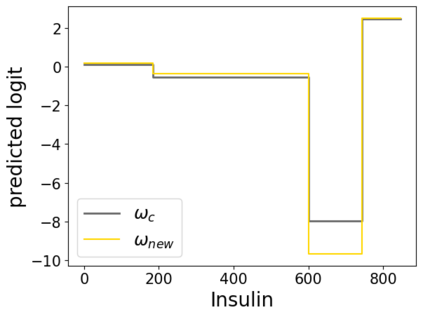
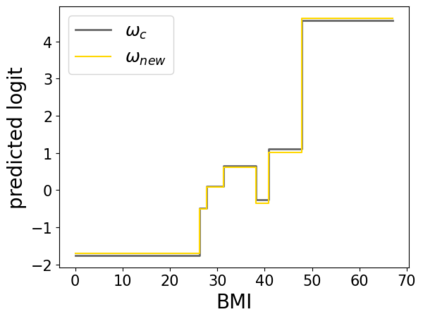
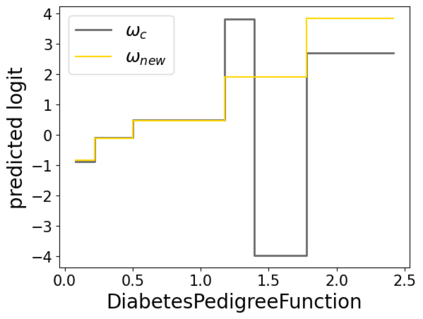
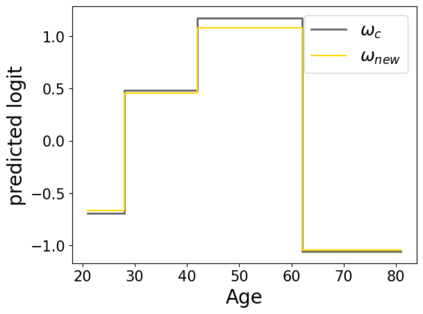
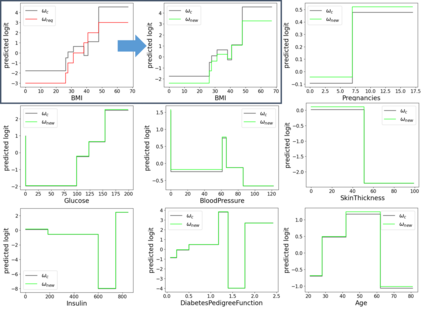
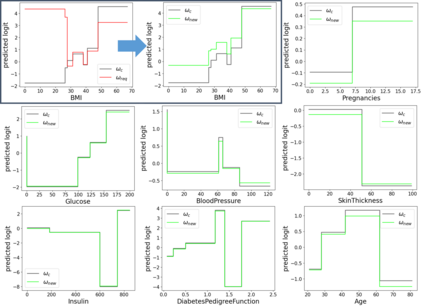
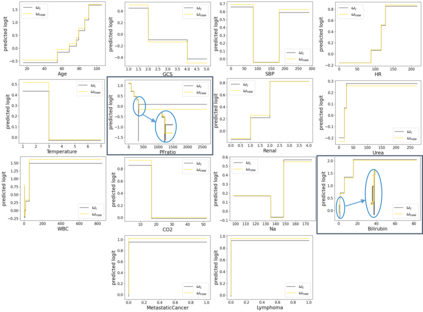
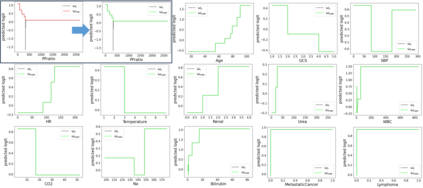
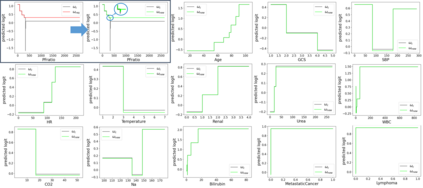
In real applications, interaction between machine learning model and domain experts is critical; however, the classical machine learning paradigm that usually produces only a single model does not facilitate such interaction. Approximating and exploring the Rashomon set, i.e., the set of all near-optimal models, addresses this practical challenge by providing the user with a searchable space containing a diverse set of models from which domain experts can choose. We present a technique to efficiently and accurately approximate the Rashomon set of sparse, generalized additive models (GAMs). We present algorithms to approximate the Rashomon set of GAMs with ellipsoids for fixed support sets and use these ellipsoids to approximate Rashomon sets for many different support sets. The approximated Rashomon set serves as a cornerstone to solve practical challenges such as (1) studying the variable importance for the model class; (2) finding models under user-specified constraints (monotonicity, direct editing); (3) investigating sudden changes in the shape functions. Experiments demonstrate the fidelity of the approximated Rashomon set and its effectiveness in solving practical challenges.
翻译:在实际应用中,机器学习模型和领域专家之间的交互至关重要。然而,通常仅生成单个模型的经典机器学习范例并不利于这种交互。通过提供可搜索的空间,其中包含多样化的模型,域专家可以从中选择,近似和探索压痕集合(即,所有近似最优模型的集合或者曰多元最优解集),可以解决这个实际挑战。我们提出一种有效且准确的方法,来近似稀疏的广义加性模型(GAMs)的压痕集合。我们提出了算法,用于近似GAMs的固定支持集的压痕集合,并使用这些椭球体来近似许多不同支持集的压痕集合。近似的压痕集合作为解决实际挑战的基石,例如(1)研究模型类别的变量重要性; (2)在用户指定的约束条件(单调性,直接编辑)下查找模型; (3)研究形状函数中的突变点。实验证明了近似压痕集的保真度及其在解决实际挑战中的有效性。