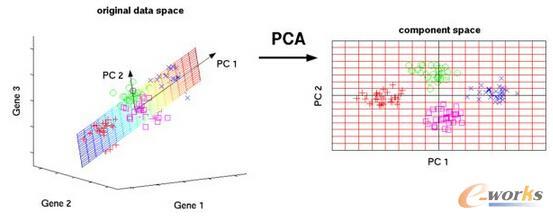
一种变量聚类方法：转置数据中的K-means及其与主成分分析的关系 (An Approach to Variable Clustering: K-means in Transposed Data and its Relationship with Principal Component Analysis)

from arxiv, Presented at conference and to appear in the proceedings of the 2025 IEEE Chilean Conference on Electrical, Electronics Engineering, Information and Communication Technologies (ChileCon)

Principal Component Analysis (PCA) and K-means constitute fundamental techniques in multivariate analysis. Although they are frequently applied independently or sequentially to cluster observations, the relationship between them, especially when K-means is used to cluster variables rather than observations, has been scarcely explored. This study seeks to address this gap by proposing an innovative method that analyzes the relationship between clusters of variables obtained by applying K-means on transposed data and the principal components of PCA. Our approach involves applying PCA to the original data and K-means to the transposed data set, where the original variables are converted into observations. The contribution of each variable cluster to each principal component is then quantified using measures based on variable loadings. This process provides a tool to explore and understand the clustering of variables and how such clusters contribute to the principal dimensions of variation identified by PCA.

翻译：主成分分析（PCA）和K-means是多元分析中的基础技术。尽管它们常被独立或顺序应用于观测聚类，但二者之间的关系——尤其是当K-means用于聚类变量而非观测时——鲜有研究。本研究通过提出一种创新方法填补这一空白，该方法分析在转置数据上应用K-means得到的变量聚类与PCA主成分之间的关系。我们的方法包括对原始数据应用PCA，并对转置数据集（原始变量转换为观测）应用K-means。随后基于变量载荷的度量，量化每个变量聚类对每个主成分的贡献。这一过程为探索和理解变量聚类，以及此类聚类如何贡献于PCA识别的主要变异维度提供了工具。