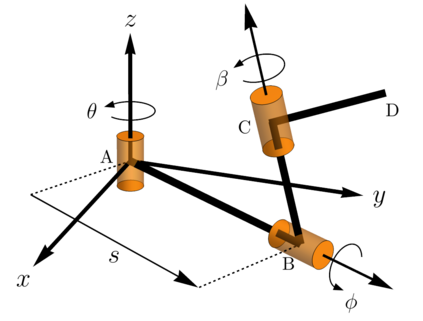
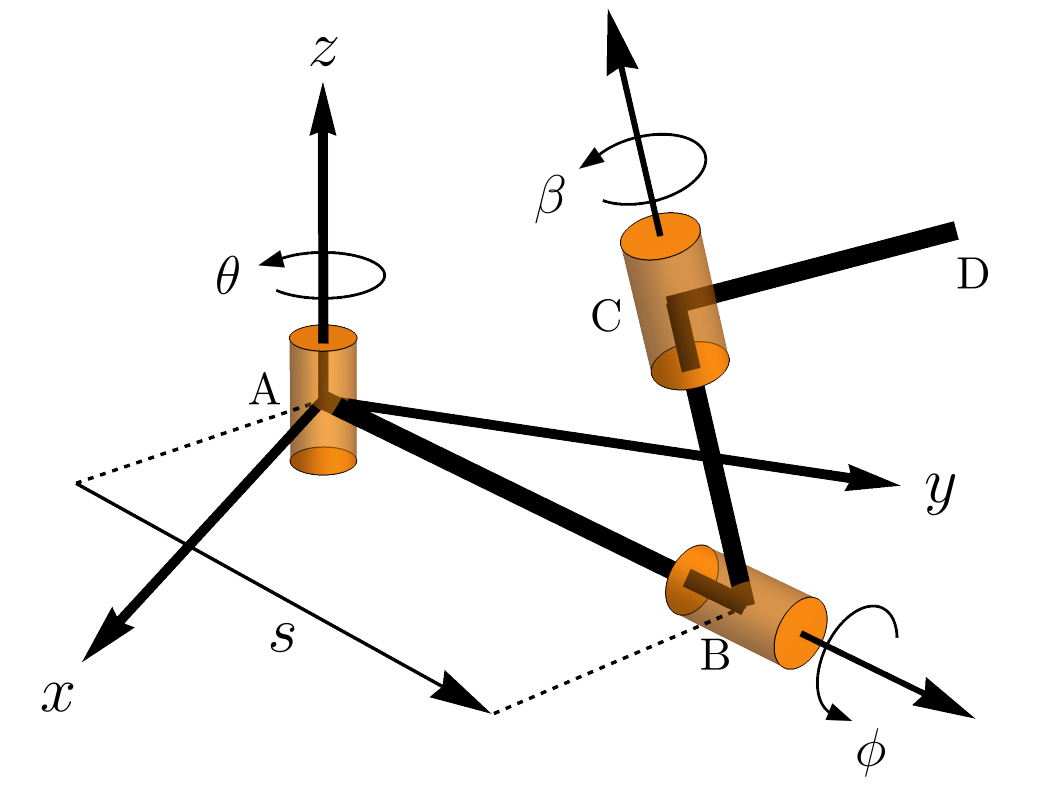
This contribution proposes a new formulation to efficiently compute directional derivatives of order one to fourth. The formulation is based on automatic differentiation implemented with dual numbers. Directional derivatives are particular cases of symmetric multilinear forms; therefore, using their symmetric properties and their coordinate representation, we implement functions to calculate mixed partial derivatives. Moreover, with directional derivatives, we deduce concise formulas for the velocity, acceleration, jerk, and jounce/snap vectors. The utility of our formulation is proved with three examples. The first example presents a comparison against the forward mode of finite differences to compute the fourth-order directional derivative of a scalar function. To this end, we have coded the finite differences method to calculate partial derivatives until the fourth order, to any order of approximation. The second example presents efficient computations of the velocity, acceleration, jerk, and jounce/snap. Finally, the third example is related to the computation of some partial derivatives. The implemented code of the proposed formulation and the finite differences method is proportioned as additional material to this article.
翻译:暂无翻译