Adaptive Bin Packing with Overflow

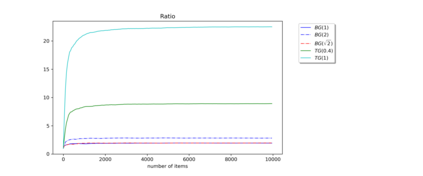
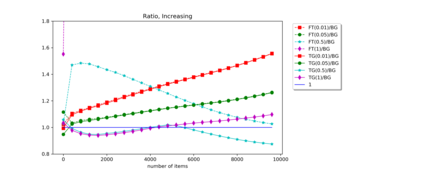
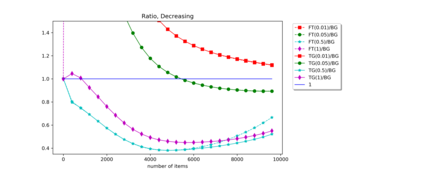
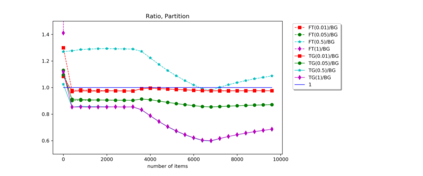
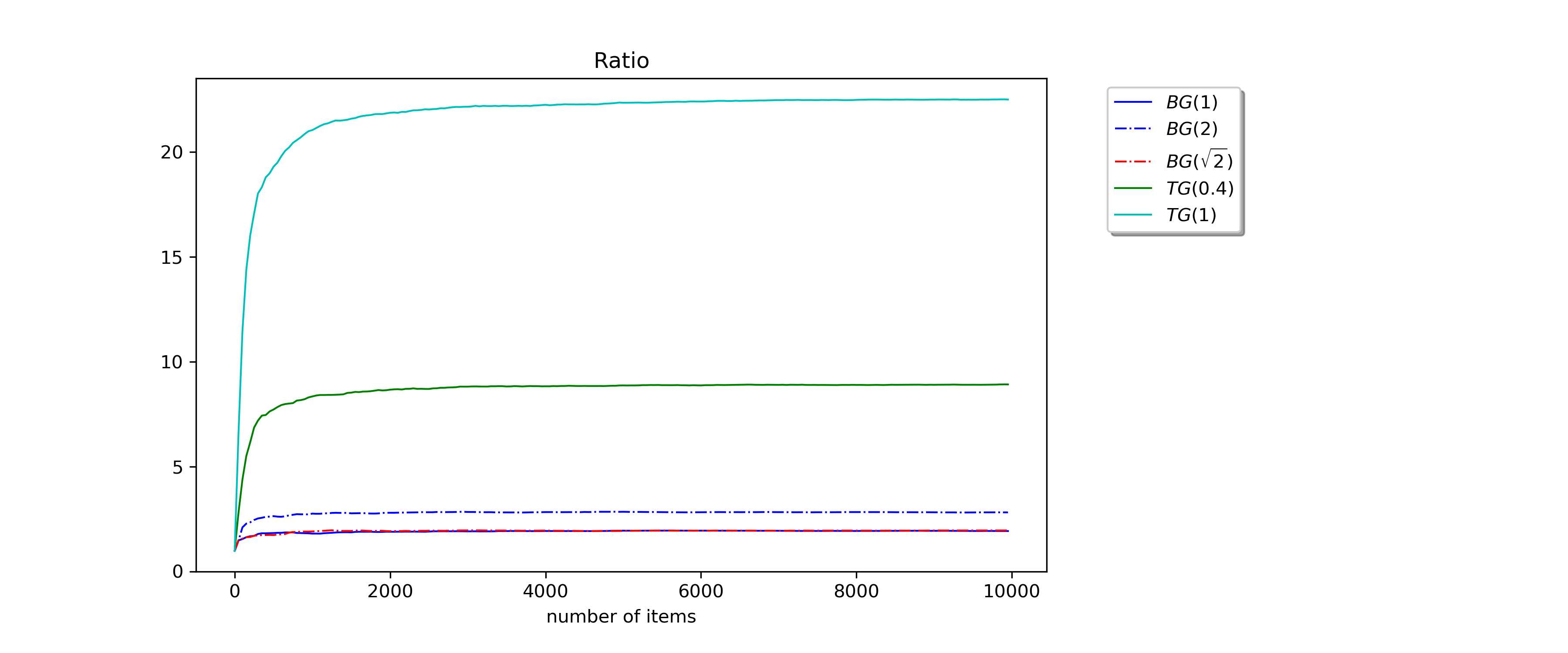
Motivated by bursty bandwidth allocation and by the allocation of virtual machines to servers in the cloud, we consider the online problem of packing items with random sizes into unit-capacity bins. Items arrive sequentially, but upon arrival an item's actual size is unknown; only its probabilistic information is available to the decision maker. Without knowing this size, the decision maker must irrevocably pack the item into an available bin or place it in a new bin. Once packed in a bin, the decision maker observes the item's actual size, and overflowing the bin is a possibility. An overflow incurs a large penalty cost and the corresponding bin is unusable for the rest of the process. In practical terms, this overflow models delayed services, failure of servers, and/or loss of end-user goodwill. The objective is to minimize the total expected cost given by the sum of the number of opened bins and the overflow penalty cost. We present an online algorithm with expected cost at most a constant factor times the cost incurred by the optimal packing policy when item sizes are drawn from an i.i.d. sequence of unknown length. We give a similar result when item size distributions are exponential with arbitrary rates. We also study the offline model, where distributions are known in advance but must be packed sequentially. We construct a soft-capacity PTAS for this problem, and show that the complexity of computing the optimal offline cost is $\#\mathbf{P}$-hard. Finally, we provide an empirical study of our online algorithm's performance.