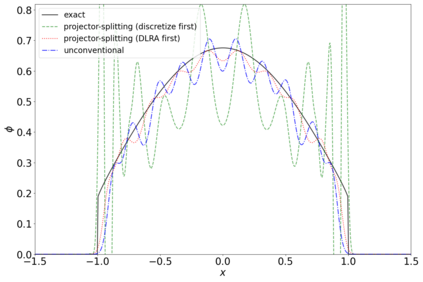
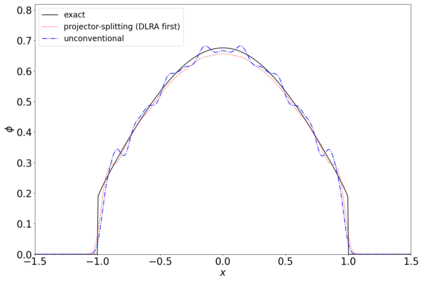
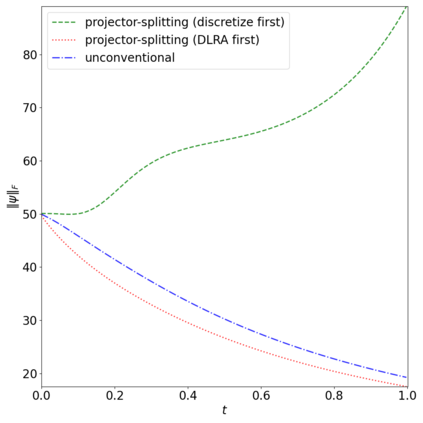
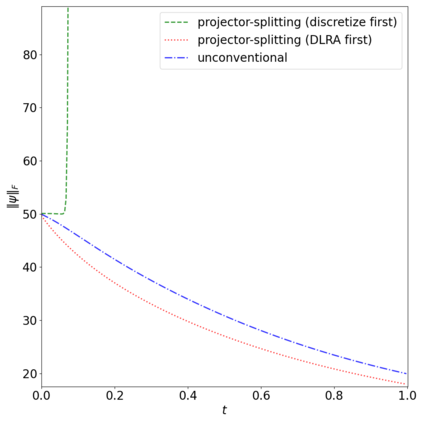
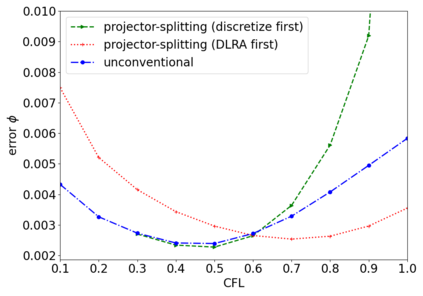
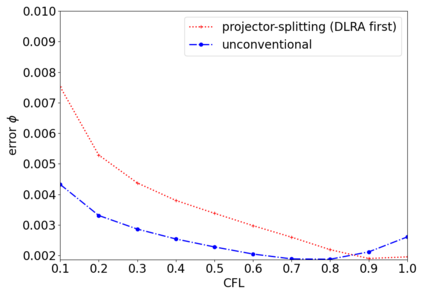
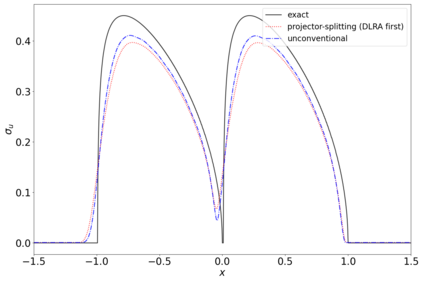
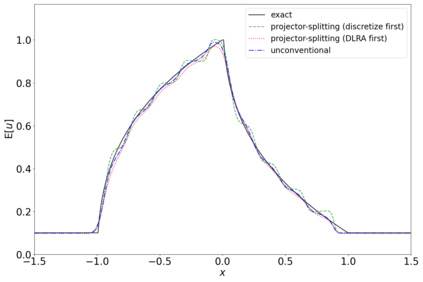
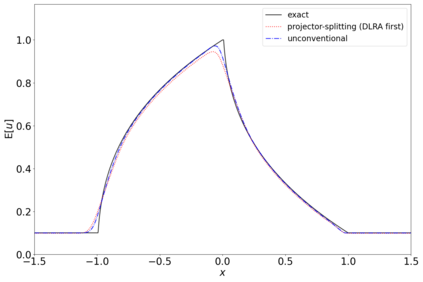
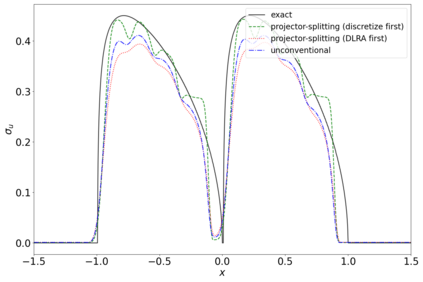
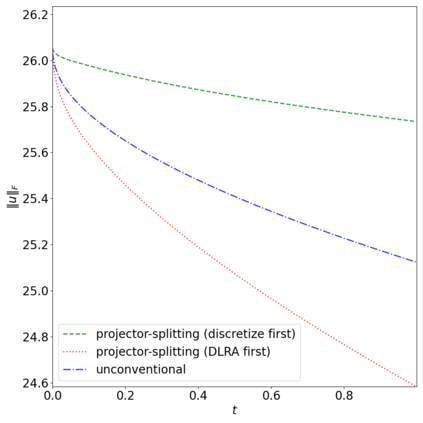
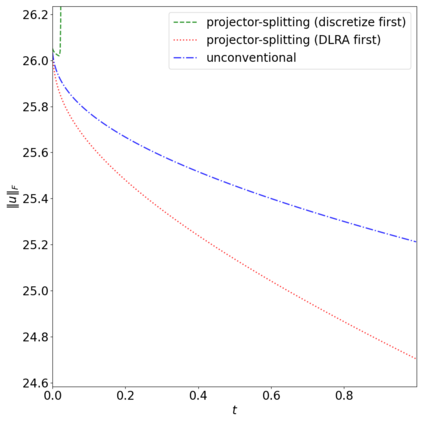
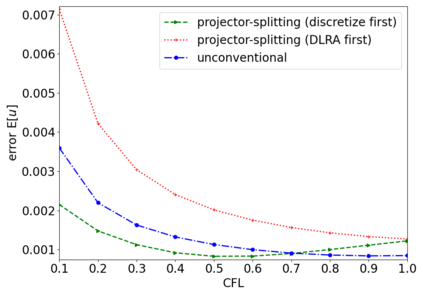
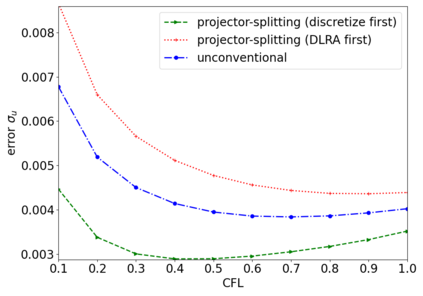
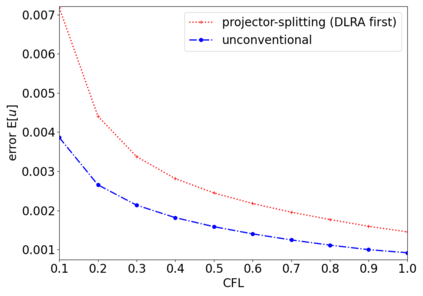
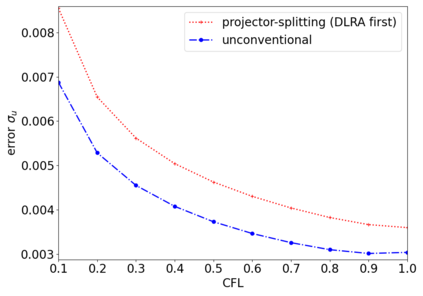
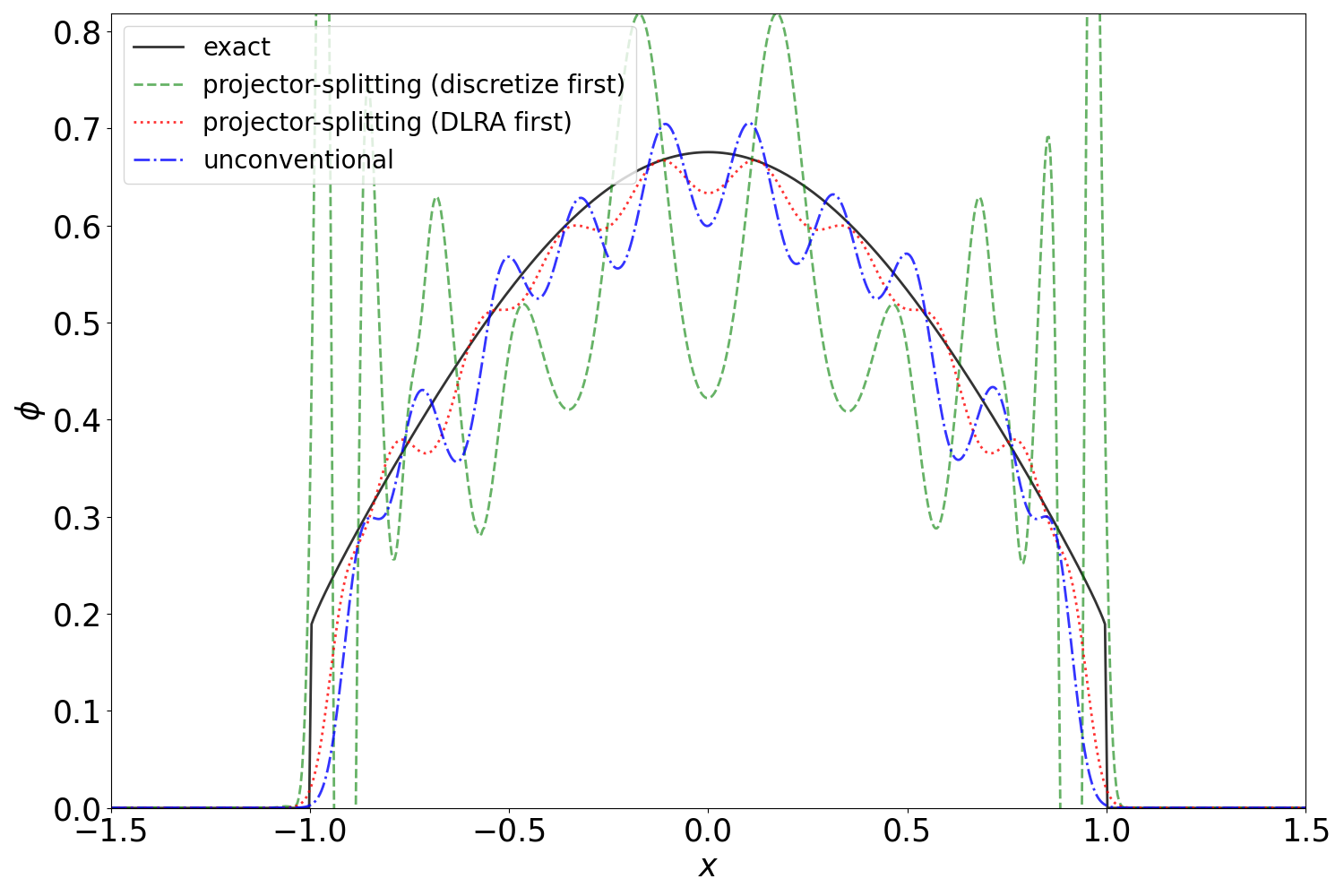
The dynamical low-rank approximation (DLRA) is used to treat high-dimensional problems that arise in such diverse fields as kinetic transport and uncertainty quantification. Even though it is well known that certain spatial and temporal discretizations when combined with the DLRA approach can result in numerical instability, this phenomenon is poorly understood. In this paper we perform a $L^2$ stability analysis for the corresponding nonlinear equations of motion. This reveals the source of the instability for the projector splitting integrator when first discretizing the equations and then applying the DLRA. Based on this we propose a projector splitting integrator, based on applying DLRA to the continuous system before performing the discretization, that recovers the classic CFL condition. We also show that the unconventional integrator has more favorable stability properties and explain why the projector splitting integrator performs better when approximating higher moments, while the unconventional integrator is generally superior for first order moments. Furthermore, an efficient and stable dynamical low-rank update for the scattering term in kinetic transport is proposed. Numerical experiments for kinetic transport and uncertainty quantification, which confirm the results of the stability analysis, are presented.
翻译:动态低位近似( DLART) 用于处理在动能传输和不确定性量化等不同领域出现的高维问题。 尽管众所周知, 与 DLAD 方法结合时, 某些空间和时间的分解可能会导致数字不稳定, 但这种现象却不易理解。 在本文中, 我们对相应的非线性运动方程式进行2美元的稳定分析。 这揭示了投影器分离整合器不稳定的根源, 最初将方程式分解, 然后应用 DLA 。 基于此, 我们提议在进行离散之前将 DLA 应用到连续系统, 从而恢复典型的 CFL 条件。 我们还表明, 非传统的分解器具有更有利的稳定性特性, 并解释了投影器分离器在适应更高时为何效果更好, 而非常规的分解器通常在第一顺序时刻处于优势状态。 此外, 我们提议, 高效和稳定的动态低级分解器在移动运输中进行连续的分解, 并提议进行 稳定性分析。