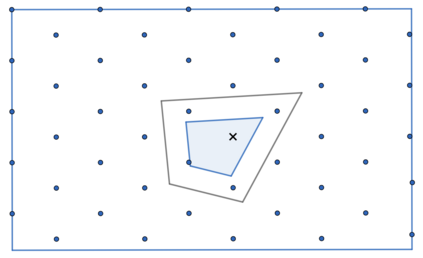
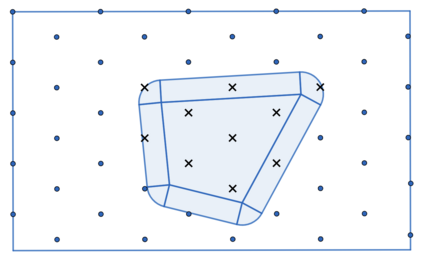
According to Haar's Theorem, every compact group $G$ admits a unique (regular, right and) left-invariant Borel probability measure $\mu_G$. Let the Haar integral (of $G$) denote the functional $\int_G:\mathcal{C}(G)\ni f\mapsto \int f\,d\mu_G$ integrating any continuous function $f:G\to\mathbb{R}$ with respect to $\mu_G$. This generalizes, and recovers for the additive group $G=[0;1)\mod 1$, the usual Riemann integral: computable (cmp. Weihrauch 2000, Theorem 6.4.1), and of computational cost characterizing complexity class #P$_1$ (cmp. Ko 1991, Theorem 5.32). We establish that in fact every computably compact computable metric group renders the Haar integral computable: once asserting computability using an elegant synthetic argument, exploiting uniqueness in a computably compact space of probability measures; and once presenting and analyzing an explicit, imperative algorithm based on 'maximum packings' with rigorous error bounds and guaranteed convergence. Regarding computational complexity, for the groups $\mathcal{SO}(3)$ and $\mathcal{SU}(2)$ we reduce the Haar integral to and from Euclidean/Riemann integration. In particular both also characterize #P$_1$. Implementation and empirical evaluation using the iRRAM C++ library for exact real computation confirms the (thus necessary) exponential runtime.
翻译:根据Haar的Theorem(G) (G)\ ni f\ maspsto\ f\,d\ mu_ G$) 和任何连续函数整合的 $f: G\to\ mathb{R} 美元。 这个概略和添加组的美元[0;1]\ mod 1 的回收成本。 通常的 Riemann 集成(G$ $ G$ ) 表示功能 $\ int_ G: g:\ f\ massal{C} (G)\ ni f\ mappsto\ f\ f\,d\ mu_ G$ (G) (I) 结合任何连续函数 $f: G\ t\ t\ ma\ mathb{R} 美元 (G) 。 这个总化和回收值为 添加组的 $[0; 通常的 Riemann 集成集成集成值 1 : 利用可调化的Creaxalalalalalalalalalalizal1 和精确度的运算算算算法 。