Revisiting the Approximate Carathéodory Problem via the Frank-Wolfe Algorithm

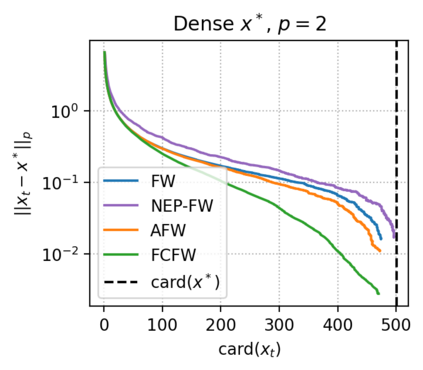
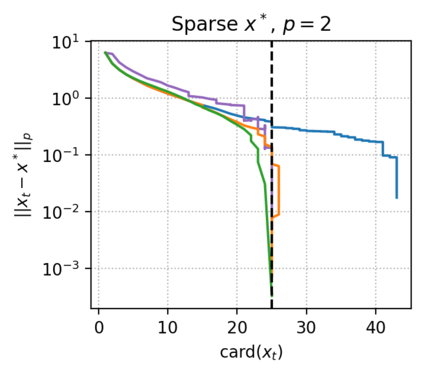
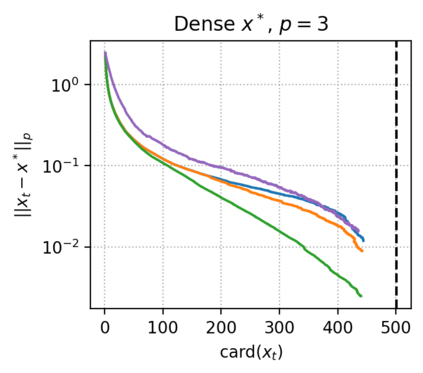
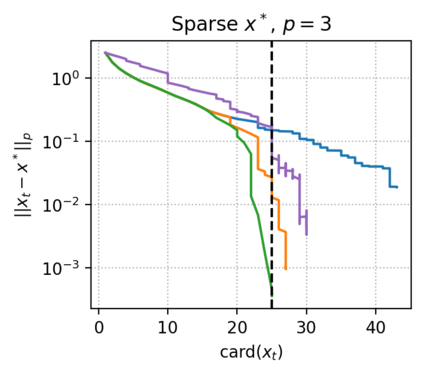
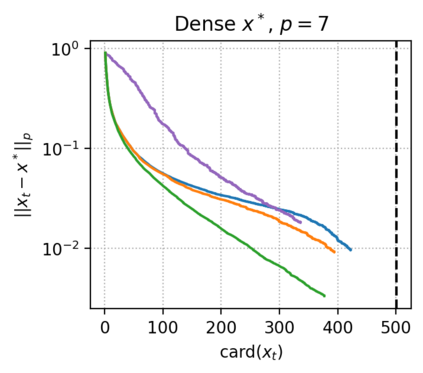
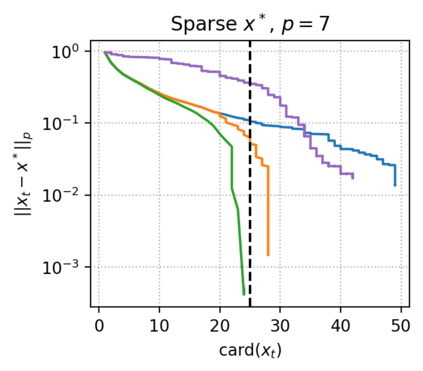
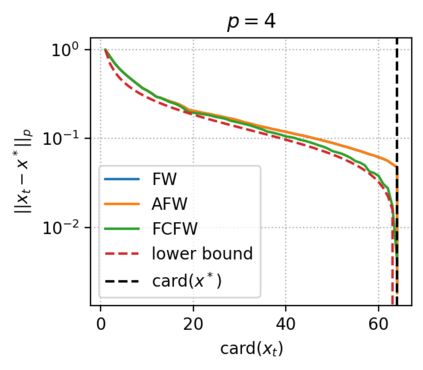
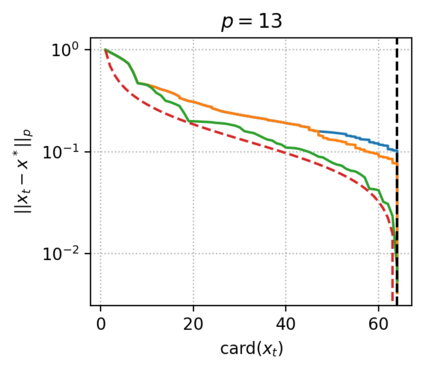
The approximate Carath\'eodory theorem states that given a compact convex set $\mathcal{C}\subset\mathbb{R}^n$ and $p\in\left[2,+\infty\right[$, each point $x^*\in\mathcal{C}$ can be approximated to $\epsilon$-accuracy in the $\ell_p$-norm as the convex combination of $\mathcal{O}(pD_p^2/\epsilon^2)$ vertices of $\mathcal{C}$, where $D_p$ is the diameter of $\mathcal{C}$ in the $\ell_p$-norm. A solution satisfying these properties can be built using probabilistic arguments or by applying mirror descent to the dual problem. We revisit the approximate Carath\'eodory problem by solving the primal problem via the Frank-Wolfe algorithm, providing a simplified analysis and leading to an efficient practical method. Furthermore, improved cardinality bounds are derived naturally using existing convergence rates of the Frank-Wolfe algorithm in different scenarios, when $x^*$ is in the (relative) interior of $\mathcal{C}$, when $x^*$ is the convex combination of a subset of vertices with small diameter, or when $\mathcal{C}$ is uniformly convex. We also propose cardinality bounds when $p\in\left[1,2\right[\cup\{+\infty\}$ via a nonsmooth variant of the algorithm. Lastly, we address the problem of finding sparse approximate projections onto $\mathcal{C}$ in the $\ell_p$-norm, $p\in\left[1,+\infty\right]$.