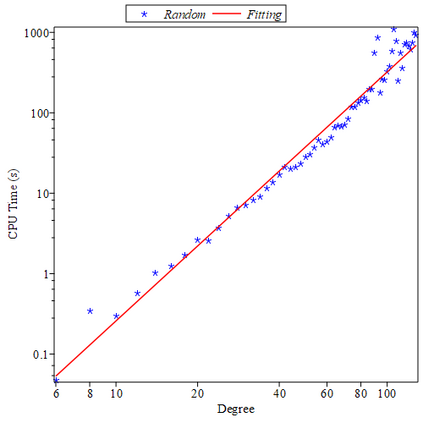
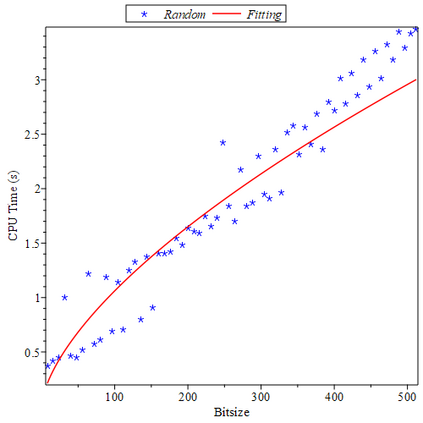
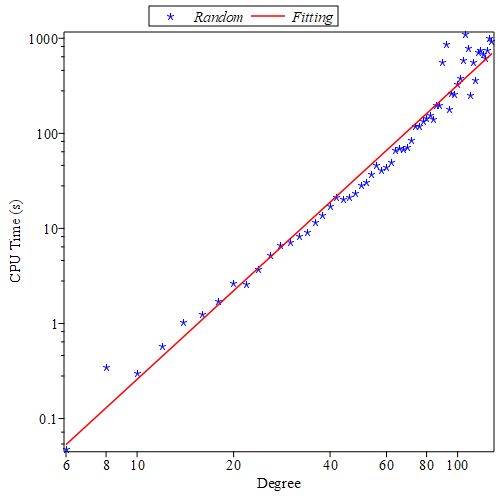
We present a new approach using differential invariants to detect projective equivalences and symmetries between two rational parametric $3D$ curves properly parametrized. In order to do this, we introduce two differential invariants that commute with M\"obius transformations, which are the transformations in the parameter space associated with the projective equivalences between the curves. The M\"obius transformations are found by first computing the gcd of two polynomials built from the differential invariants, and then searching for the M\"obius-like factors of this gcd. The projective equivalences themselves are easily computed from the M\"obius transformations. In particular, and unlike previous approaches, we avoid solving big polynomial systems. The algorithm has been implemented in Maple, and evidences of its efficiency as well as a comparison with previous approaches are given.
翻译:我们提出了一个新的方法,使用差异变量来检测两个合理的3D美元曲线之间的预测等值和对称性。 为了做到这一点, 我们引入了两种差异变量, 与 M\“ obius 变换, 即与曲线之间的预测等值相关的参数空间变换。 M\ “ obius 变换” 是通过首先计算两个从差异变异中构建的多元值的格子, 然后查找这个 gcd 的 M\“ obius 类似因素 ” 。 投影等值本身很容易从 M\ “ obius 变换中计算出来。 特别是, 与以往的方法不同, 我们避免解决大多数值系统。 算法已经在Maple 中实施, 并且提供了其效率的证据以及与先前方法的比较。