Linear Regression for Power Law Distribution Fitting

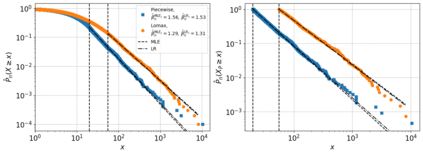
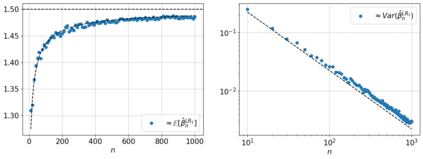
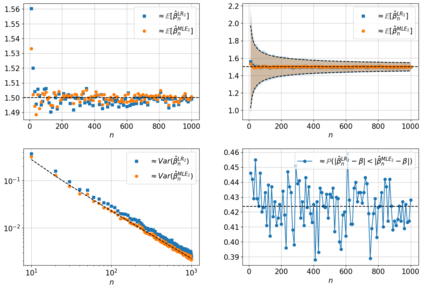
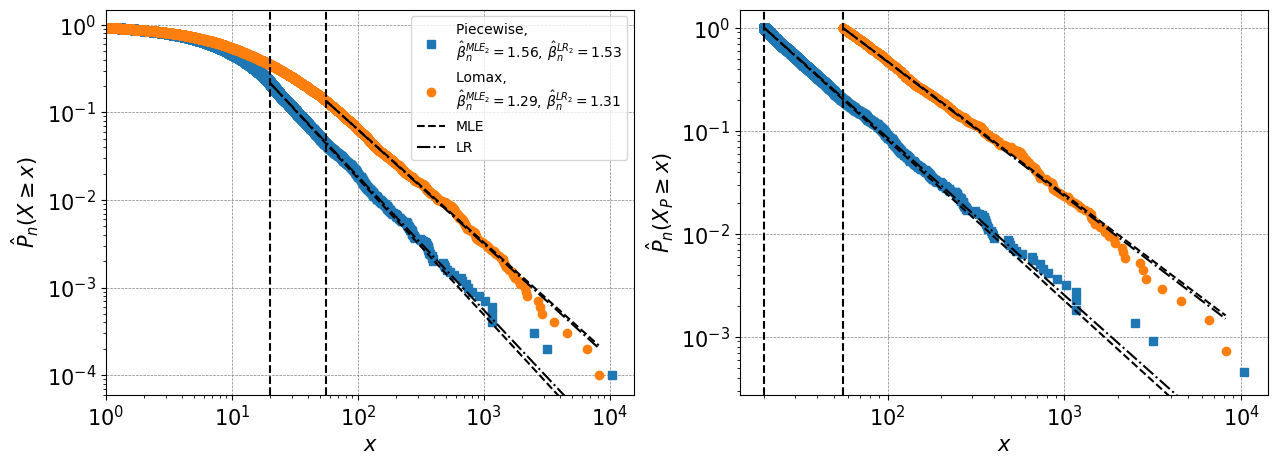
We fit the exponent of the Pareto distribution, that is equivalent or can approximate the continuous power law distribution given a cutoff point, using linear regression (LR). We use LR on the logged variables of the empirical tail (one minus the empirical cumulative distribution function). We find the distribution of the consistent LR estimator and an approximate sigmoid relationship of the mean that underestimates the exponent. By factoring out a sigmoid function used to approximate the mean we transform the LR estimator so it is approximately unbiased with variance comparable to the minimum variance unbiased transformed MLE estimator.