Sparsistent filtering of comovement networks from high-dimensional data

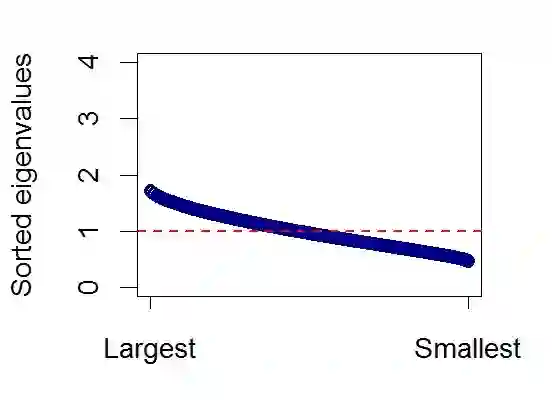
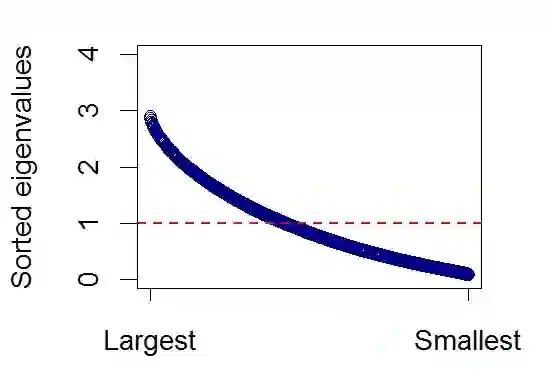
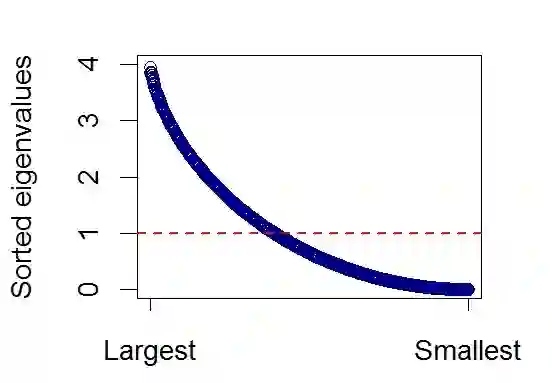
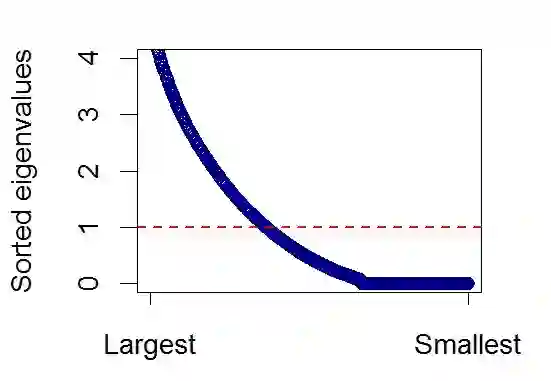
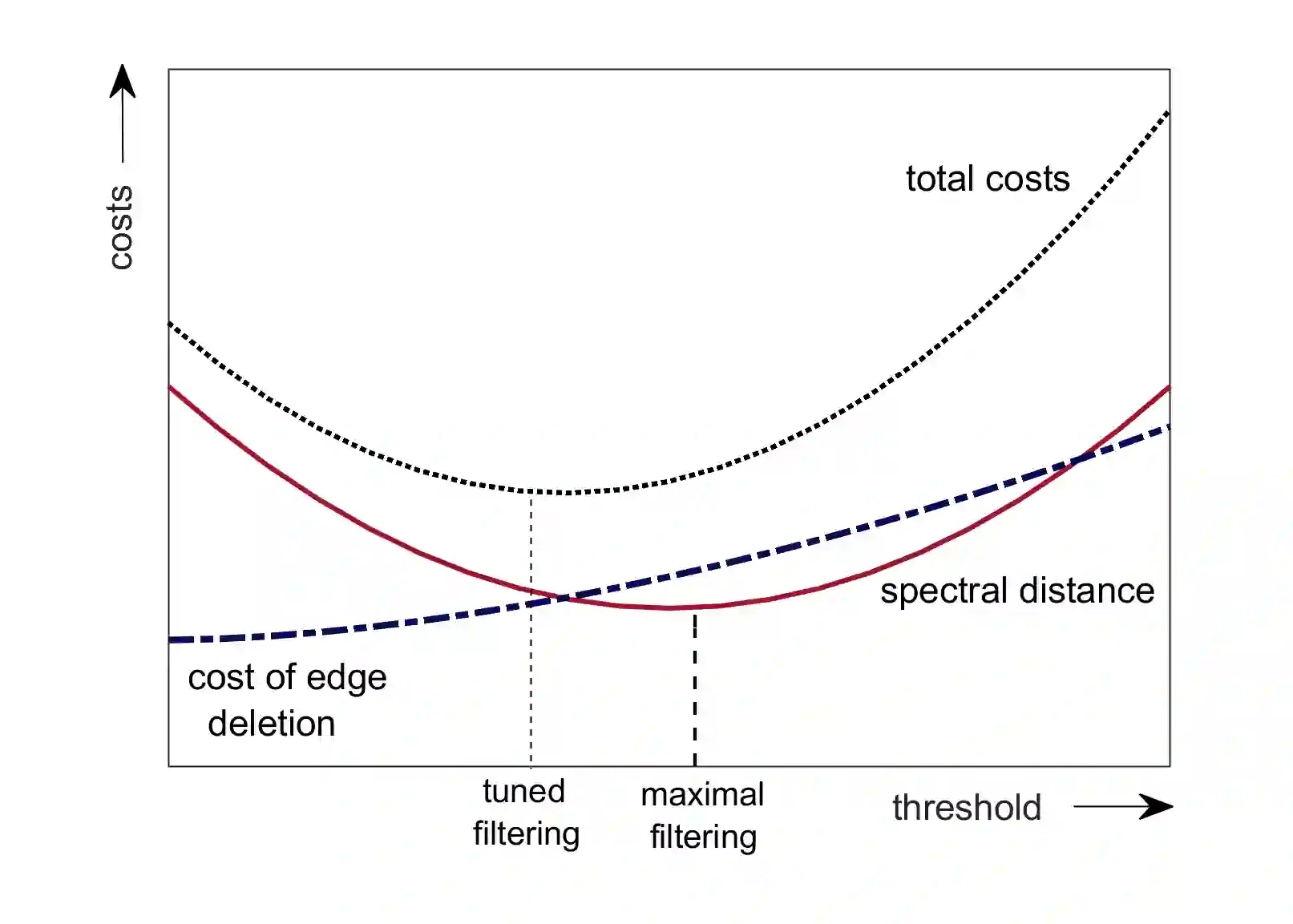
Network filtering is an important form of dimension reduction to isolate the core constituents of large and interconnected complex systems. We introduce a new technique to filter large dimensional networks arising out of dynamical behavior of the constituent nodes, exploiting their spectral properties. As opposed to the well known network filters that rely on preserving key topological properties of the realized network, our method treats the spectrum as the fundamental object and preserves spectral properties. Applying asymptotic theory for high dimensional data for the filter, we show that it can be tuned to interpolate between zero filtering to maximal filtering that induces sparsity and consistency while having the least spectral distance from a linear shrinkage estimator. We apply our proposed filter to covariance networks constructed from financial data, to extract the key subnetwork embedded in the full sample network.