Fast training and sampling of Restricted Boltzmann Machines

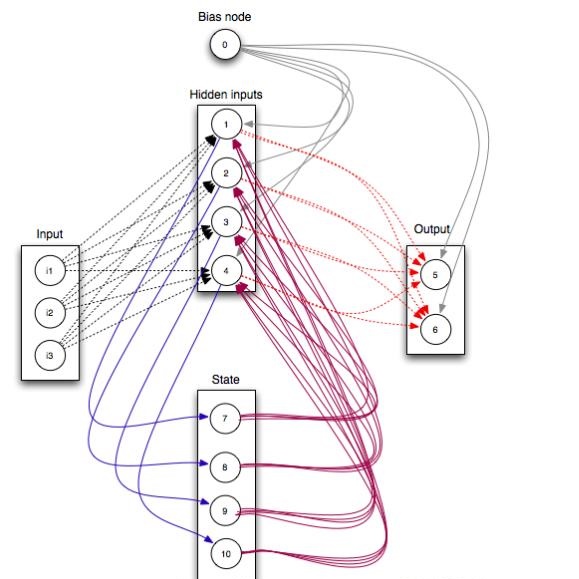
Restricted Boltzmann Machines (RBMs) are powerful tools for modeling complex systems and extracting insights from data, but their training is hindered by the slow mixing of Markov Chain Monte Carlo (MCMC) processes, especially with highly structured datasets. In this study, we build on recent theoretical advances in RBM training and focus on the stepwise encoding of data patterns into singular vectors of the coupling matrix, significantly reducing the cost of generating new samples and evaluating the quality of the model, as well as the training cost in highly clustered datasets. The learning process is analogous to the thermodynamic continuous phase transitions observed in ferromagnetic models, where new modes in the probability measure emerge in a continuous manner. We leverage the continuous transitions in the training process to define a smooth annealing trajectory that enables reliable and computationally efficient log-likelihood estimates. This approach enables online assessment during training and introduces a novel sampling strategy called Parallel Trajectory Tempering (PTT) that outperforms previously optimized MCMC methods. To mitigate the critical slowdown effect in the early stages of training, we propose a pre-training phase. In this phase, the principal components are encoded into a low-rank RBM through a convex optimization process, facilitating efficient static Monte Carlo sampling and accurate computation of the partition function. Our results demonstrate that this pre-training strategy allows RBMs to efficiently handle highly structured datasets where conventional methods fail. Additionally, our log-likelihood estimation outperforms computationally intensive approaches in controlled scenarios, while the PTT algorithm significantly accelerates MCMC processes compared to conventional methods.