Query-points visibility constraint minimum link paths in simple polygons

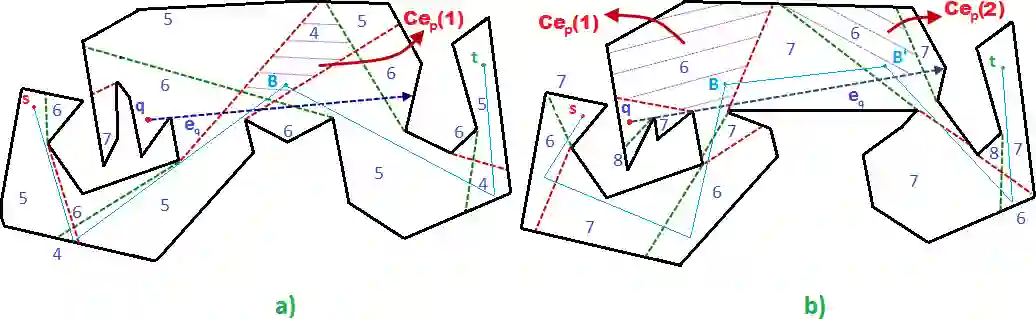
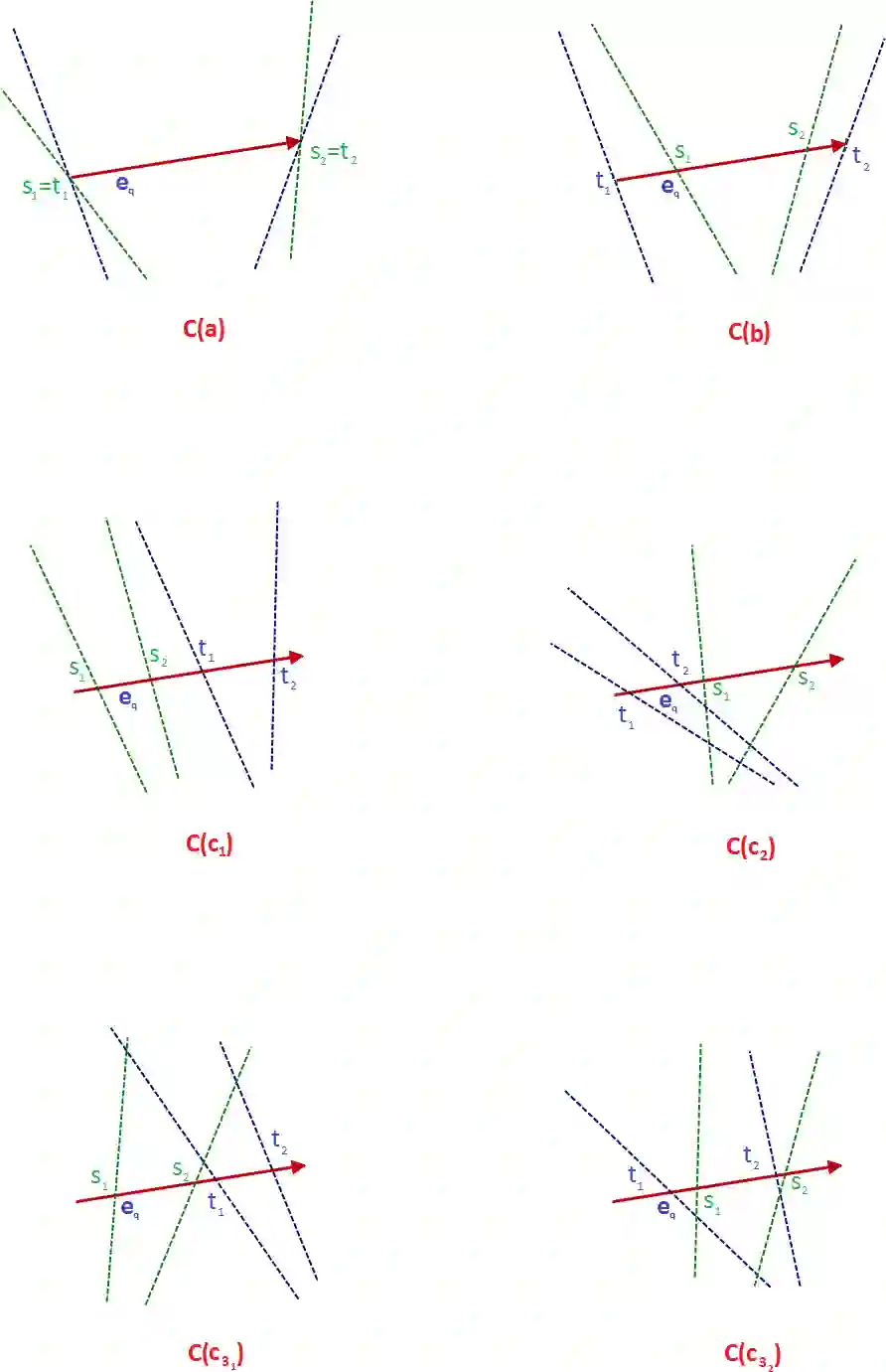
We study the query version of constrained minimum link paths between two points inside a simple polygon with $n$ vertices such that there is at least one point on the path, visible from a query point. Initially, we solve this problem for two given points $s$, $t$ and a query point $q$. Then, the proposed solution is extended to a general case for three arbitrary query points $s$, $t$ and $q$. In the former, we propose an algorithm with $O(n)$ preprocessing time. Extending this approach for the latter case, we develop an algorithm with $O(n^3)$ preprocessing time. The link distance of a $q$-$visible$ path between $s$, $t$ as well as the path are provided in time $O(\log n)$ and $O(k+\log n)$, respectively, for the above two cases, where $k$ is the number of links.