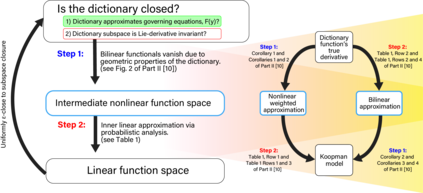
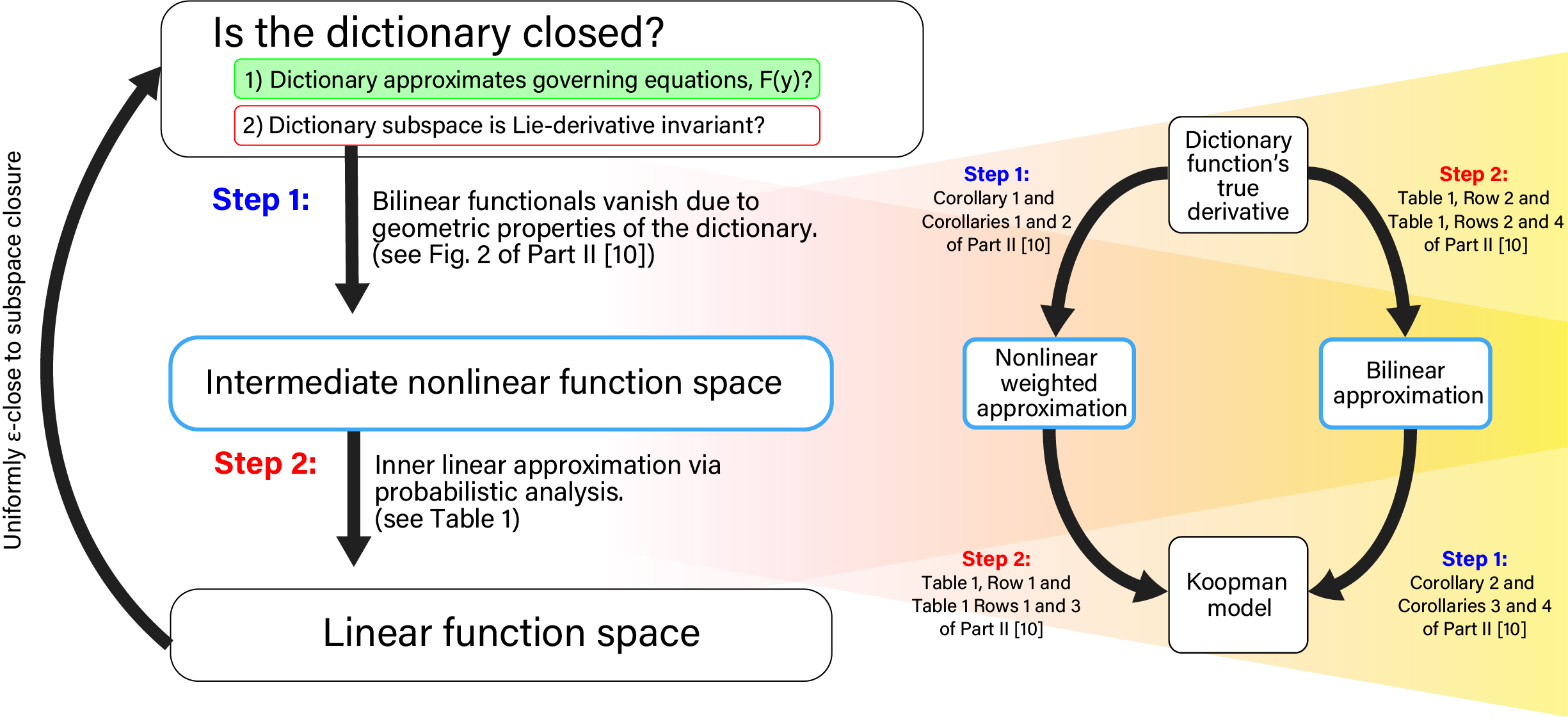
Koopman operators model nonlinear dynamics as a linear dynamic system acting on a nonlinear function as the state. This nonstandard state is often called a Koopman observable and is usually approximated numerically by a superposition of functions drawn from a dictionary. In a widely used algorithm, Extended Dynamic Mode Decomposition, the dictionary functions are drawn from a fixed class of functions. Recently, deep learning combined with EDMD has been used to learn novel dictionary functions in an algorithm called deep dynamic mode decomposition (deepDMD). The learned representation both (1) accurately models and (2) scales well with the dimension of the original nonlinear system. In this paper we analyze the learned dictionaries from deepDMD and explore the theoretical basis for their strong performance. We explore State-Inclusive Logistic Lifting (SILL) dictionary functions to approximate Koopman observables. Error analysis of these dictionary functions show they satisfy a property of subspace approximation, which we define as uniform finite approximate closure. Our results provide a hypothesis to explain the success of deep neural networks in learning numerical approximations to Koopman operators. Part 2 of this paper will extend this explanation by demonstrating the subspace invariant of heterogeneous dictionaries and presenting a head-to-head numerical comparison of deepDMD and low-parameter heterogeneous dictionary learning.
翻译:Koopman 操作员将非线性动态作为线性动态系统模型, 作为一种线性动态系统, 以非线性功能作为状态。 这个非标准状态通常被称为 Koopman 可观测, 通常通过从字典中提取功能的叠加来进行数字比较。 在一个广泛使用的算法中, 扩展动态模式分解, 字典功能是从固定的功能类别中提取的。 最近, 深度学习与 EDMD 结合, 用于在一种称为深动态模式分解( 深DMD) 的算法中学习小字典功能。 所学的表达式 (1) 准确的模型和 (2) 与原非线性系统层面相匹配。 在本文中, 我们分析深DMD所学的词典, 并探索其强大性能的理论基础。 我们探索国家包容性物流提升( SILL) 字典功能, 以近似Koopman 函数为基准。 错误分析这些词典功能满足了子空间近似特性, 我们将其定义为统一的有限近似关闭。 我们的结果为解释深线性网络在向 Koopman 操作者 数字近似操作者 。 。 将扩展 将扩展 度 度 度 度 度 和 度 度 度 度 的 度 度 的 的 度 度 度 的 的 度 的 校际级 校略度 校略级 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校 校