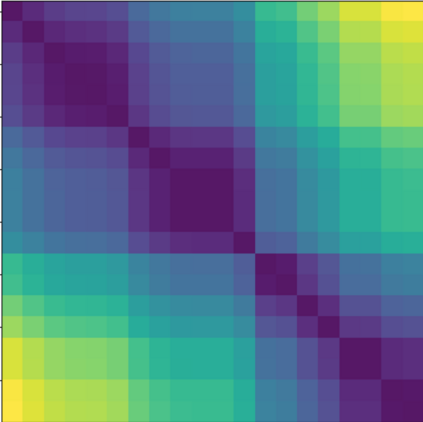
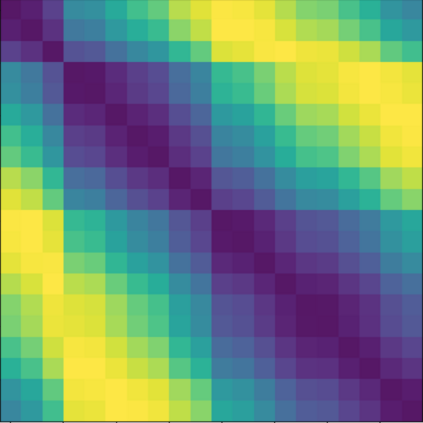
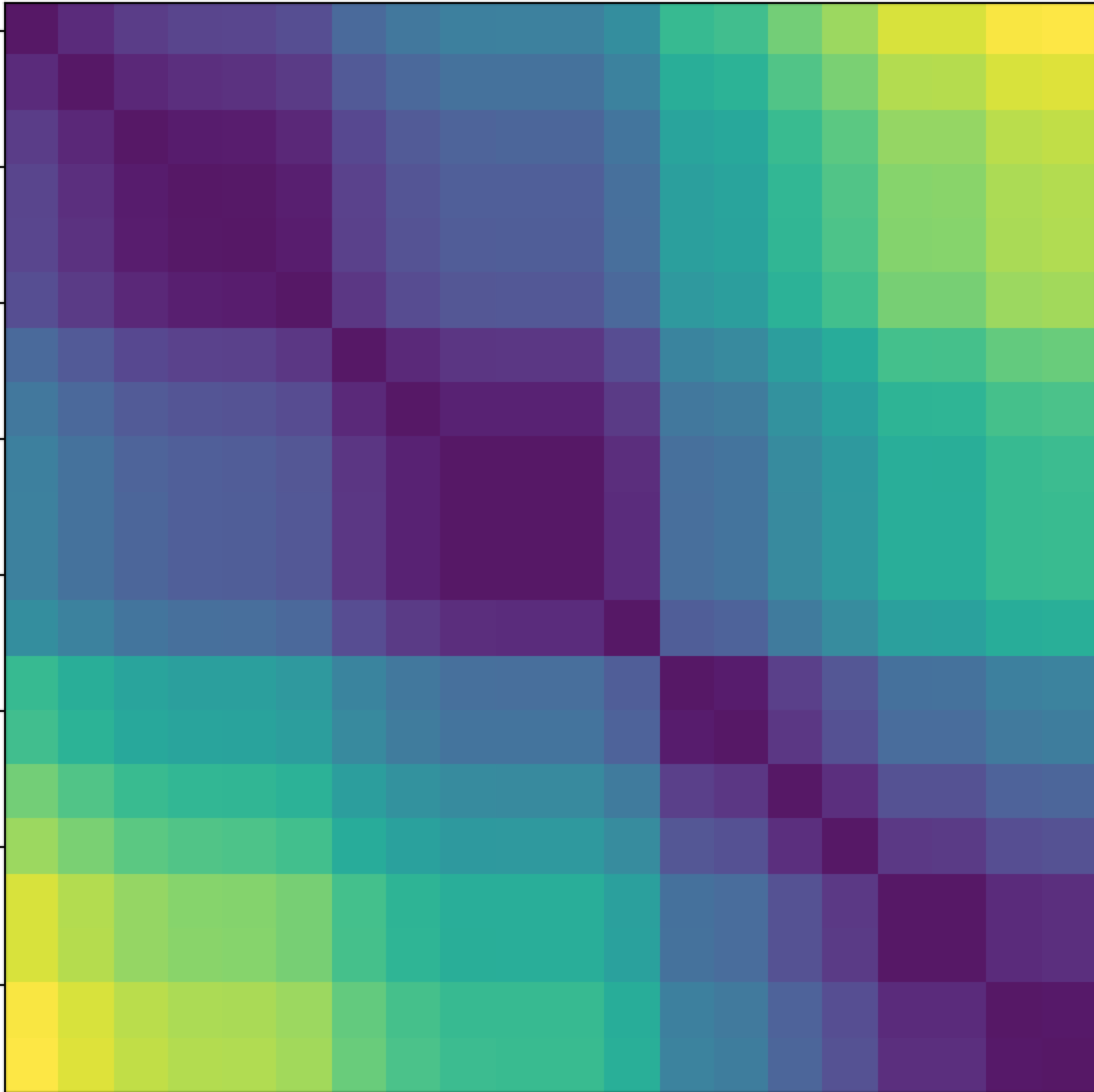
We study the problem of circular seriation, where we are given a matrix of pairwise dissimilarities between $n$ objects, and the goal is to find a {\em circular order} of the objects in a manner that is consistent with their dissimilarity. This problem is a generalization of the classical {\em linear seriation} problem where the goal is to find a {\em linear order}, and for which optimal ${\cal O}(n^2)$ algorithms are known. Our contributions can be summarized as follows. First, we introduce {\em circular Robinson matrices} as the natural class of dissimilarity matrices for the circular seriation problem. Second, for the case of {\em strict circular Robinson dissimilarity matrices} we provide an optimal ${\cal O}(n^2)$ algorithm for the circular seriation problem. Finally, we propose a statistical model to analyze the well-posedness of the circular seriation problem for large $n$. In particular, we establish ${\cal O}(\log(n)/n)$ rates on the distance between any circular ordering found by solving the circular seriation problem to the underlying order of the model, in the Kendall-tau metric.
翻译:我们研究循环演化问题,研究循环演化问题,我们得到的是美元天体之间相异的矩阵,目标是以与异性相一致的方式找到物体的 {em 循环顺序} 。 这个问题是典型的 {em 线性演化问题的一般化, 其目的在于找到 {em 线性顺序}, 并且为此我们知道最佳的 $ o}(n) 2美元算法。 我们的贡献可以概括如下。 首先,我们采用 em 通知 Robinson 矩阵 } 作为循环演化问题的自然异性矩阵类别。 其次,对于严格 Robinson 圆 异性矩阵的情况,我们为循环演化问题提供了最佳的 $ cals O} (n) 2美元算法。 最后,我们提出一个统计模型,用于分析大 美元 圆性演化问题的准确性。 特别是, 我们用 $_ caLO} (n) /n) 在任何通过解决圆形变序的基本定序的模型之间的距离上, 。