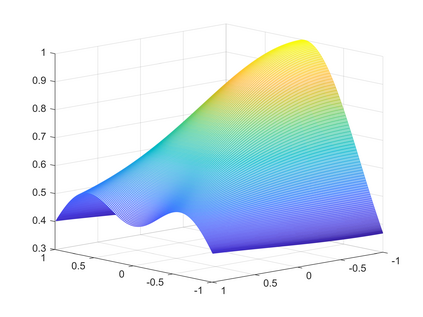
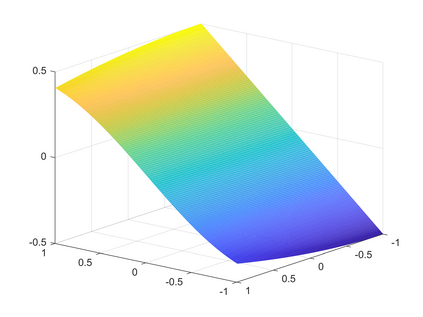
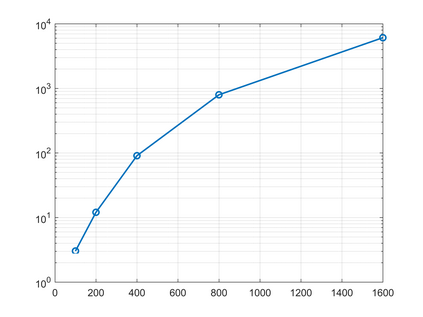
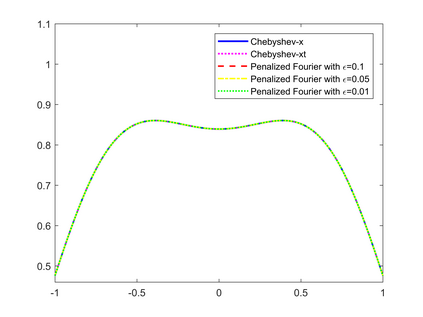
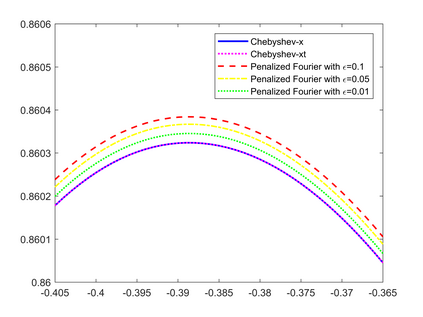
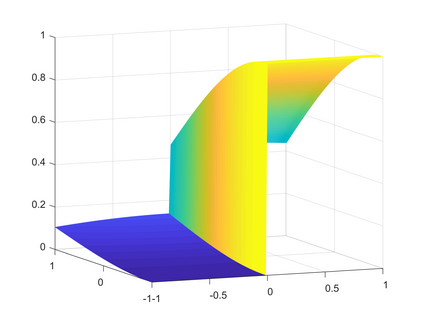
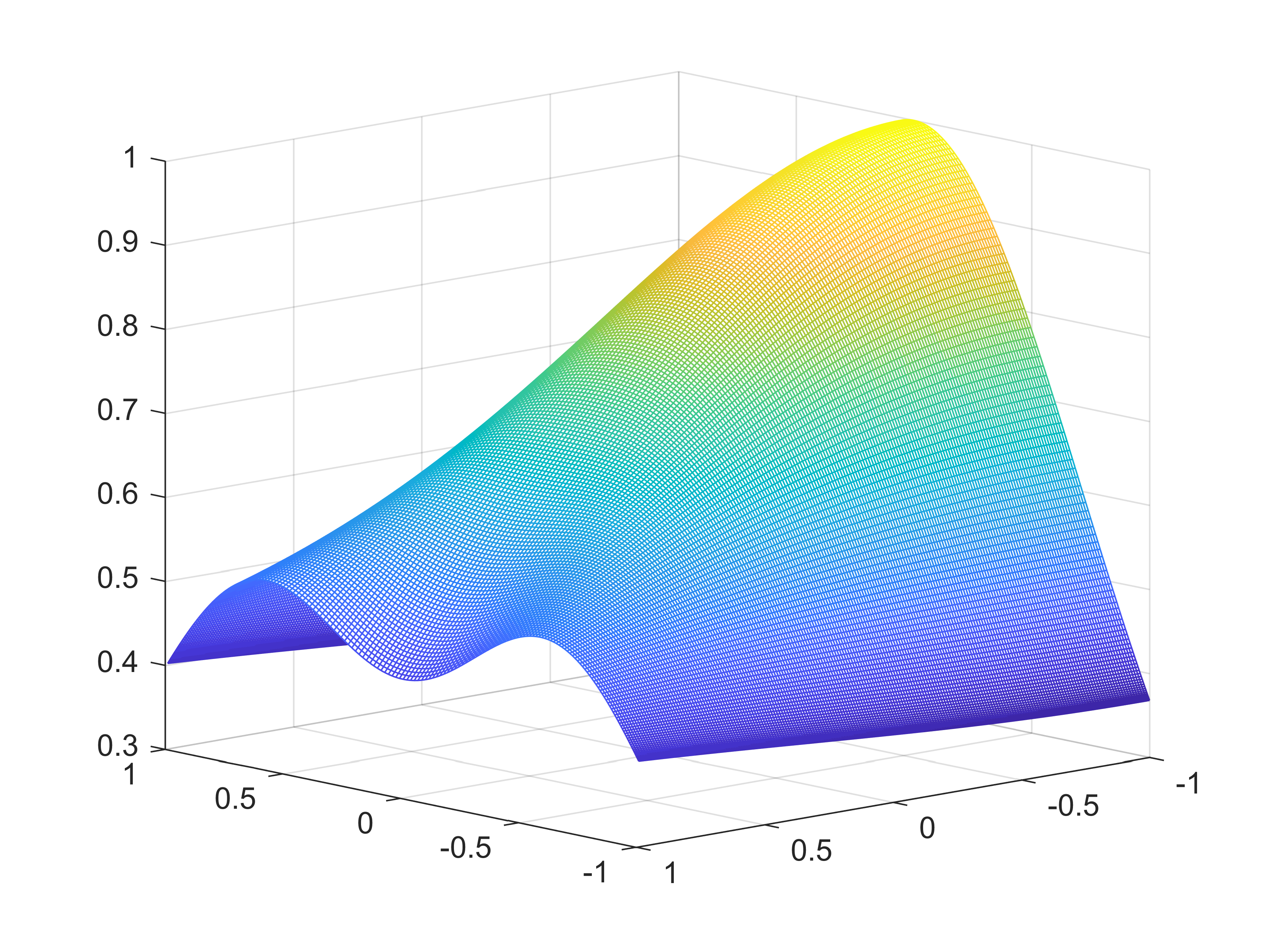
Peridynamics is a nonlocal generalization of continuum mechanics theory which adresses discontinuous problems without using partial derivatives and replacing its by an integral operator. As a consequence, it finds applications in the framework of the development and evolution of fractures and damages in elastic materials. In this paper we consider a one-dimensional nonlinear model of peridynamics and propose a suitable two-dimensional fast-convolution spectral method based on Chebyshev polynomials to solve the model. This choice allows us to gain the same accuracy both in space and time. We show the convergence of the method and perform several simulations to study the performance of the spectral scheme.
翻译:周期动力学是连续体力学理论的非局部概括,它不使用部分衍生物,而是用一个整体操作者取代它,从而在断裂和弹性材料损害的开发和演变框架内发现各种应用。在本文中,我们考虑一个单维非线性极动力学模型,并根据Chebyshev 多元分子提出一个合适的二维快速进化光谱方法来解决模型。这一选择使我们能够在空间和时间上获得同样的精确度。我们展示了该方法的趋同,并进行了若干模拟,以研究光谱图的性能。