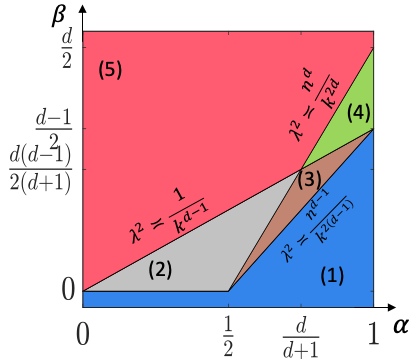
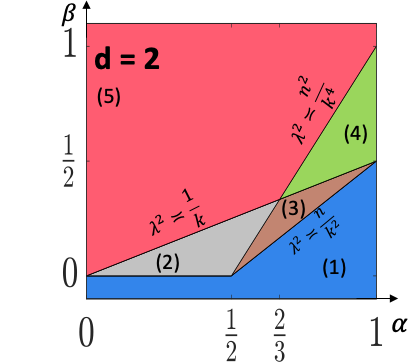
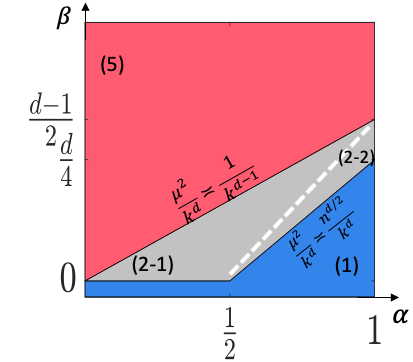
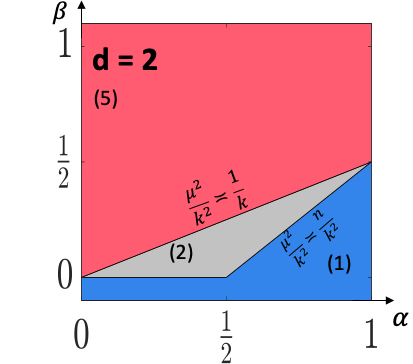
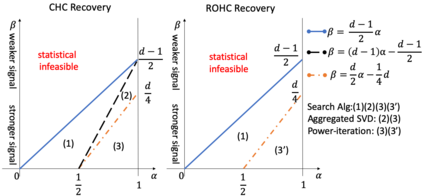
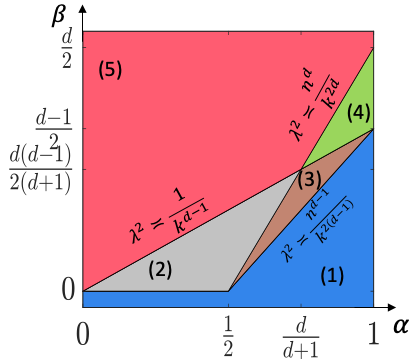
This paper studies the statistical and computational limits of high-order clustering with planted structures. We focus on two clustering models, constant high-order clustering (CHC) and rank-one higher-order clustering (ROHC), and study the methods and theory for testing whether a cluster exists (detection) and identifying the support of cluster (recovery). Specifically, we identify the sharp boundaries of signal-to-noise ratio for which CHC and ROHC detection/recovery are statistically possible. We also develop the tight computational thresholds: when the signal-to-noise ratio is below these thresholds, we prove that polynomial-time algorithms cannot solve these problems under the computational hardness conjectures of hypergraphic planted clique (HPC) detection and hypergraphic planted dense subgraph (HPDS) recovery. We also propose polynomial-time tensor algorithms that achieve reliable detection and recovery when the signal-to-noise ratio is above these thresholds. Both sparsity and tensor structures yield the computational barriers in high-order tensor clustering. The interplay between them results in significant differences between high-order tensor clustering and matrix clustering in literature in aspects of statistical and computational phase transition diagrams, algorithmic approaches, hardness conjecture, and proof techniques. To our best knowledge, we are the first to give a thorough characterization of the statistical and computational trade-off for such a double computational-barrier problem. Finally, we provide evidence for the computational hardness conjectures of HPC detection (via low-degree polynomial and Metropolis methods) and HPDS recovery (via low-degree polynomial method).
翻译:本文研究种植结构的高阶集群的统计和计算限制。 我们侧重于两个组群模型, 恒定的高阶集群和一级高阶集群(ROHC), 并研究测试集群是否存在的方法和理论(检测)和确定集集(回收)的支持。 具体地说, 我们提出了CHC和ROHC在统计上可以检测/ 回收的信号到噪音比率的精确度比界限。 我们还开发了紧凑的计算门槛: 当信号到噪音比率低于这些阈值时, 我们证明, 在高阶集聚中, 多式时段算法无法解决这些问题。 在高成像刻板(HHPC)的计算硬性猜想下, 检测和高成型种植密度子子(HPDDS) 回收。 我们还提出了当信号到噪声比率比率高于这些阈值时, 双轨和高压结构结构导致计算障碍。 在高压组合中, 高成交点的多时, 高序的计算方法, 以及我们统计结构中, 最高级的精确的计算方法 。