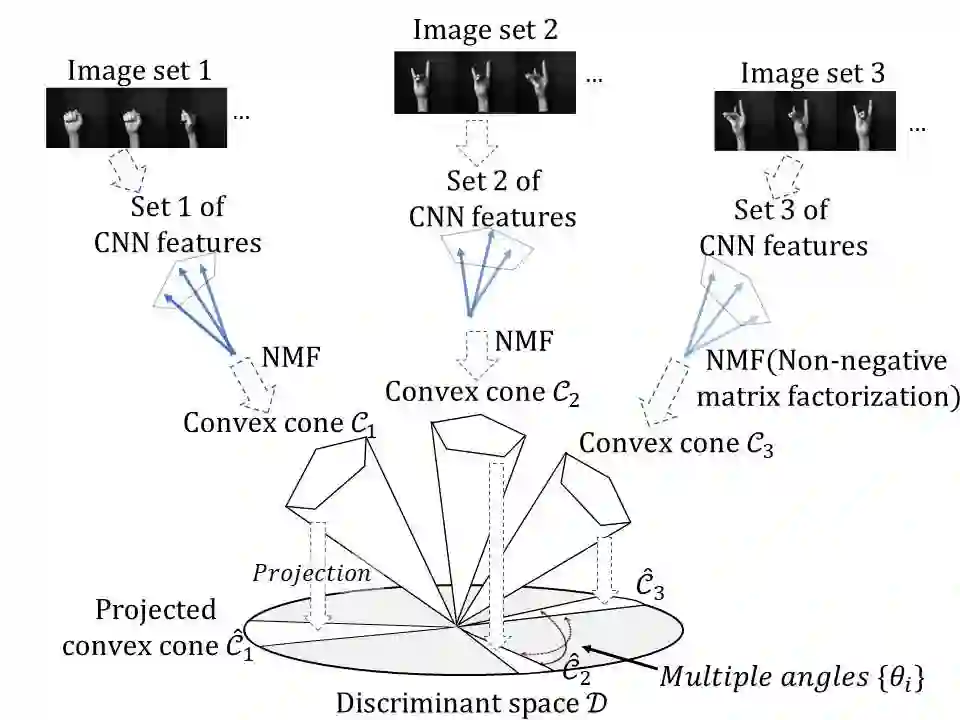
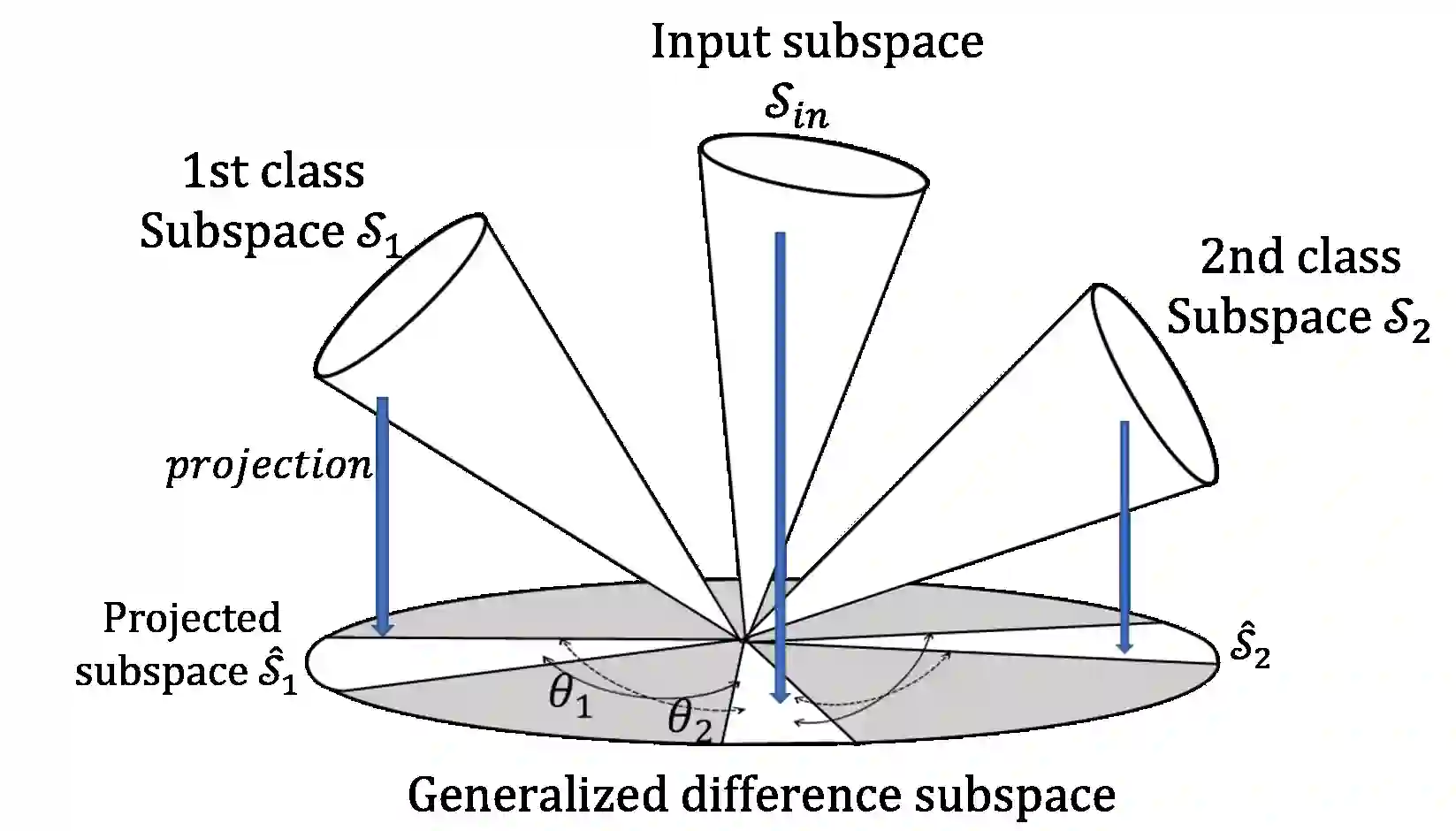
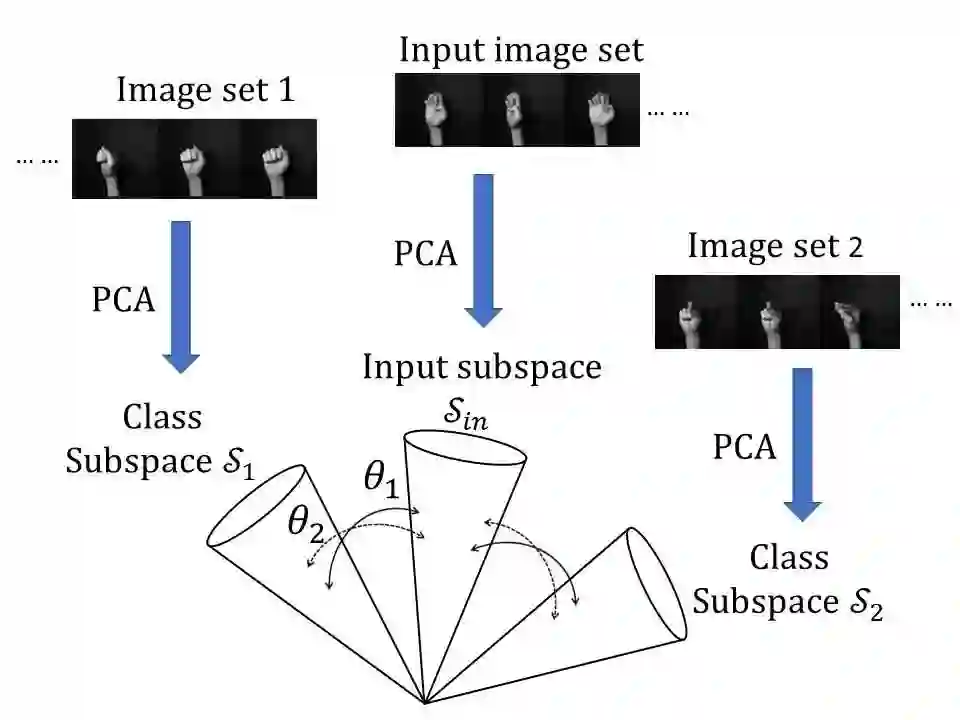
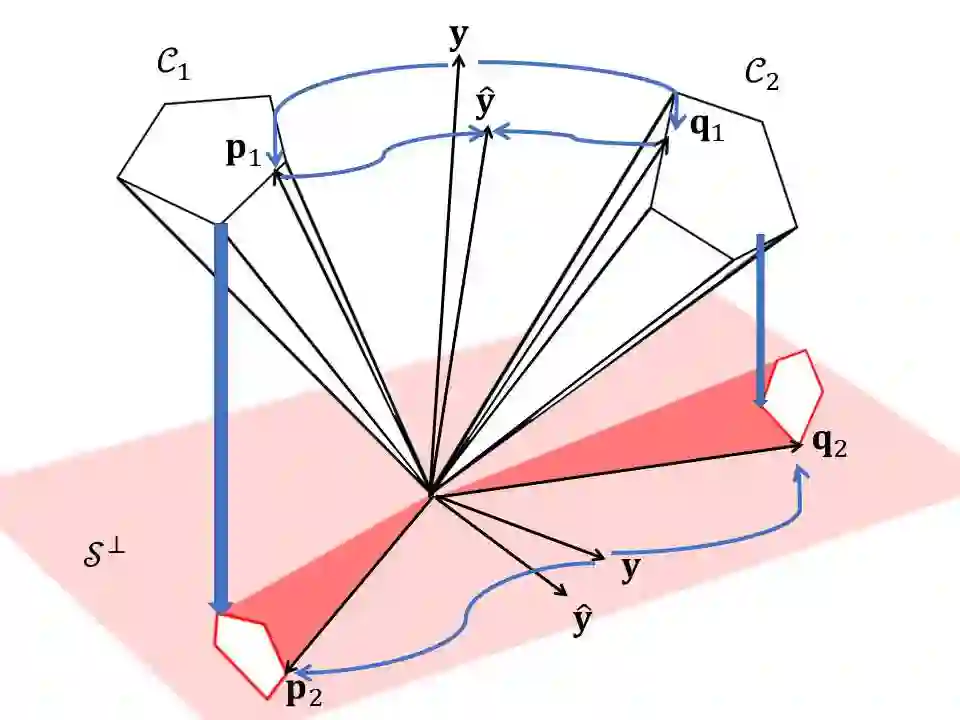
In this paper, we propose a method for image-set classification based on convex cone models. Image set classification aims to classify a set of images, which were usually obtained from video frames or multi-view cameras, into a target object. To accurately and stably classify a set, it is essential to represent structural information of the set accurately. There are various representative image features, such as histogram based features, HLAC, and Convolutional Neural Network (CNN) features. We should note that most of them have non-negativity and thus can be effectively represented by a convex cone. This leads us to introduce the convex cone representation to image-set classification. To establish a convex cone based framework, we mathematically define multiple angles between two convex cones, and then define the geometric similarity between the cones using the angles. Moreover, to enhance the framework, we introduce a discriminant space that maximizes the between-class variance (gaps) and minimizes the within-class variance of the projected convex cones onto the discriminant space, similar to the Fisher discriminant analysis. Finally, the classification is performed based on the similarity between projected convex cones. The effectiveness of the proposed method is demonstrated experimentally by using five databases: CMU PIE dataset, ETH-80, CMU Motion of Body dataset, Youtube Celebrity dataset, and a private database of multi-view hand shapes.
翻译:在本文中, 我们提出一种基于 convex 锥形模型的图像定位分类方法 。 图像定位分类旨在将通常从视频框架或多视图相机获得的图像集分类成目标对象 。 要准确和精确地分类一个数据集, 就必须准确地代表一个数据集的结构信息 。 有各种有代表性的图像特征, 如基于直方图的特征、 HLAC 和进化神经网络( CNN ) 。 我们应当指出, 其中多数图像定位具有非增强性, 从而可以通过一个 convex 锥体内流有效代表。 这导致我们引入基于图像定位分类的 convex 锥形图显示。 要建立基于 convex 的矩形框架, 我们从数学角度定义了两个 convex 锥形锥形的多个角度, 然后用角度定义锥形图的形状之间的几何相似性 。 此外, 为了加强框架, 我们引入了一种共振间空间最大程度的等级差异( gaps), 并且可以将预测的C- 矩形内矩形的内矩形图解法 。 以相同的C 分析 。 。 所 所 所 所 所 所 所 所 所 所 所 所 所 所 所 所 所 所 所 所 所 所 所 所 所 所 所 所 所 所 所 所 所 所 所 所 所 所 的 的 所 所 所 所 的 所 所 所 所 所 所 所 所 所 所 所 的 的 的 所 所 所 的 所 的 所 所 所 所 所 所 所 所 所 所 所 所 的 所 所 的 的 所 的 的 所 的 所 所 所 所 的 所 所 所 的 的 所 所 所 所 所 所 所 所 所 所 所 所 的 的 所 所 所 所 所 所 所 所 所 的 的 所 的 的 的 所 的