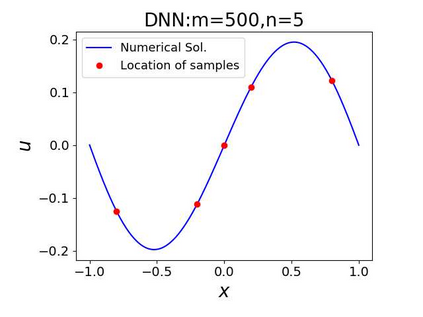
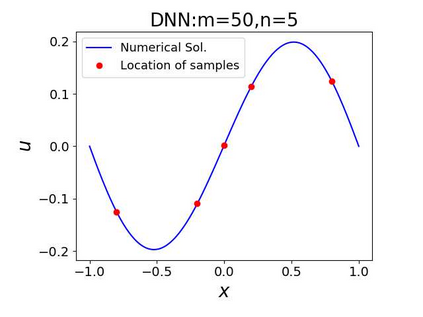
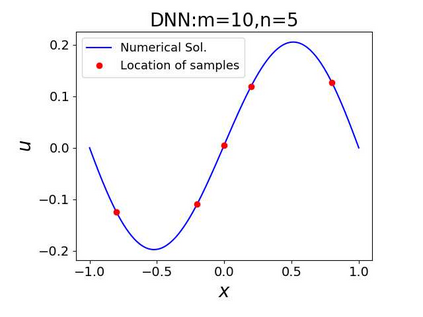
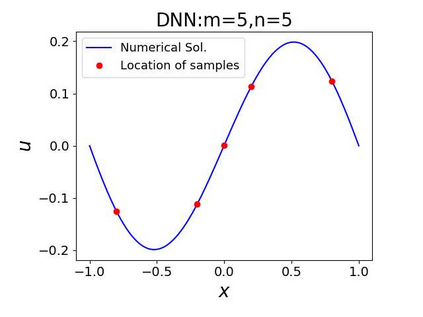
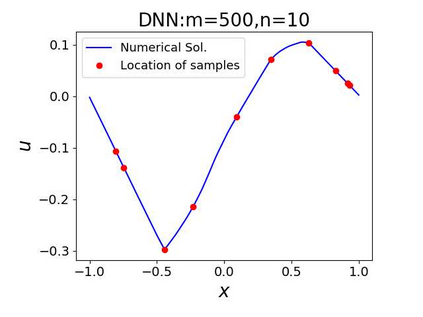
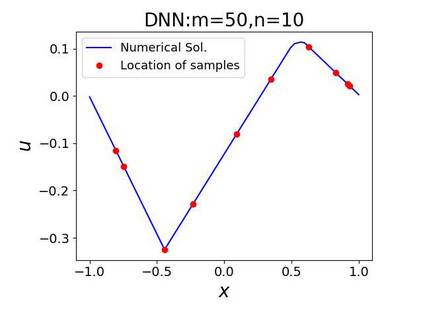
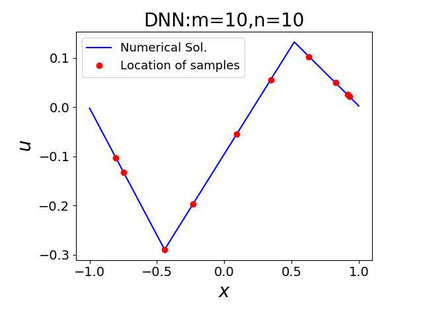
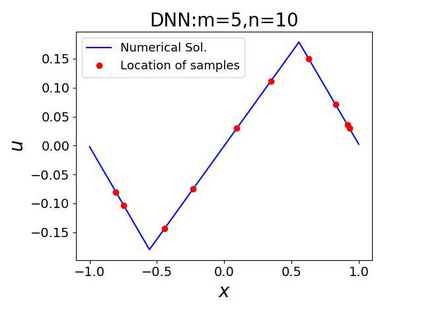
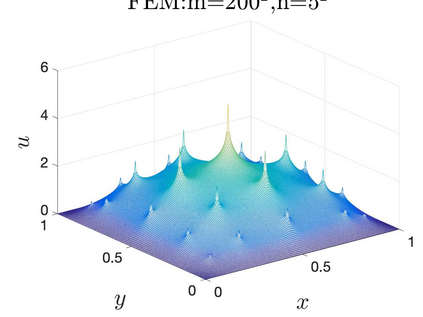
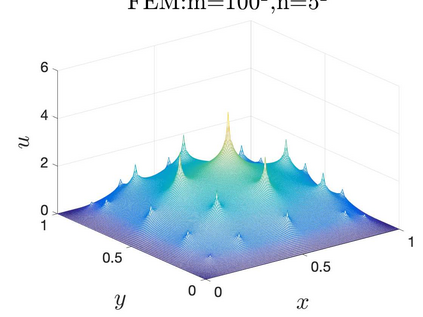
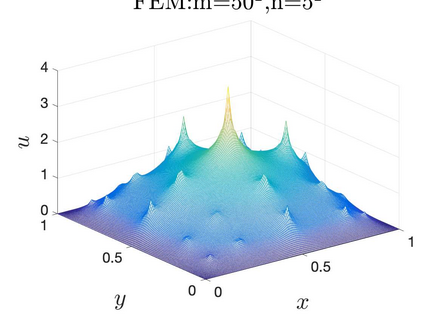
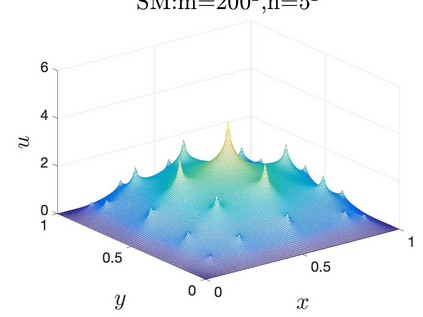
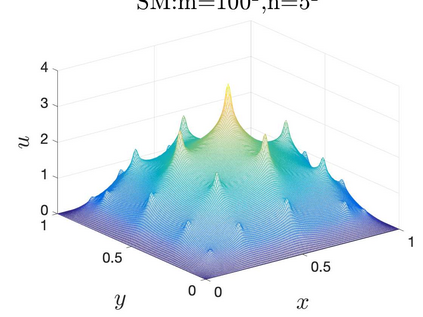
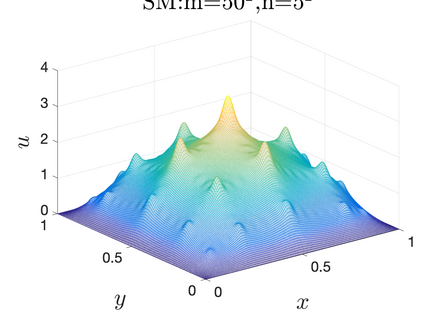
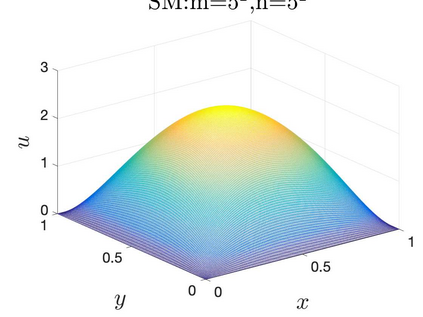
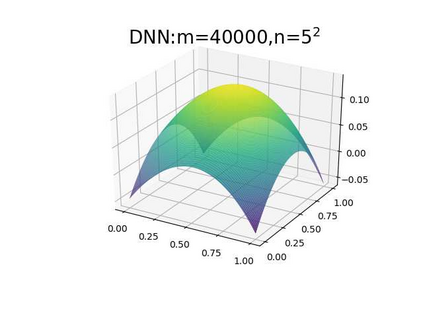
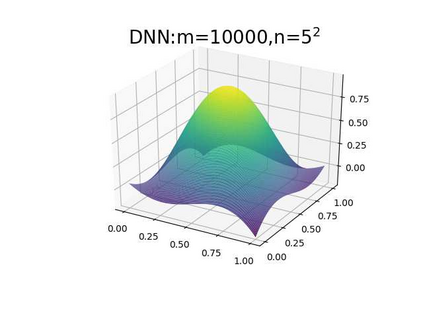
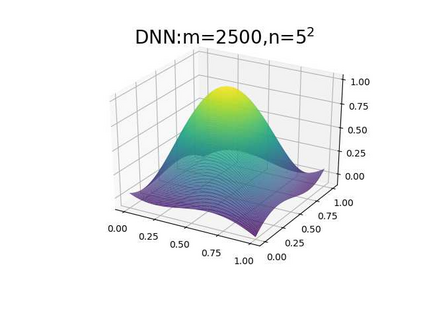
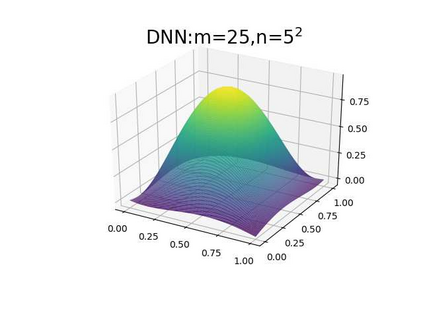
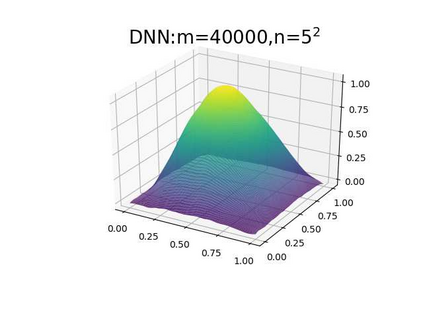
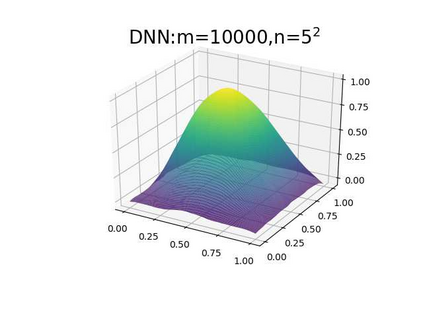
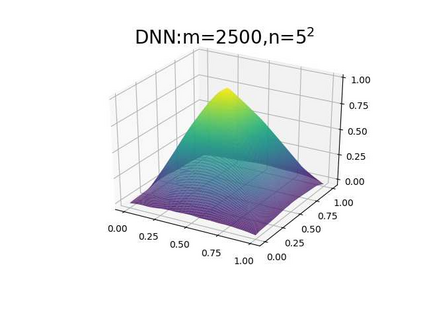
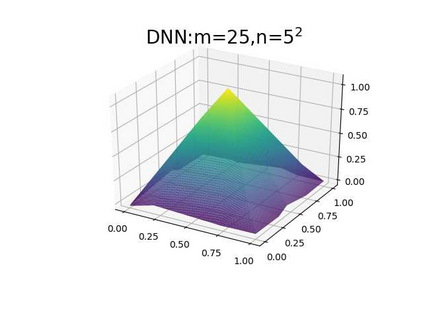
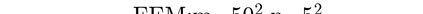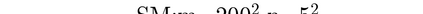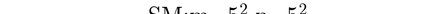This paper aims at studying the difference between Ritz-Galerkin (R-G) method and deep neural network (DNN) method in solving partial differential equations (PDEs) to better understand deep learning. To this end, we consider solving a particular Poisson problem, where the information of the right-hand side of the equation f is only available at n sample points, that is, f is known at finite sample points. Through both theoretical and numerical studies, we show that solution of the R-G method converges to a piecewise linear function for the one dimensional (1D) problem or functions of lower regularity for high dimensional problems. With the same setting, DNNs however learn a relative smooth solution regardless of the dimension, this is, DNNs implicitly bias towards functions with more low-frequency components among all functions that can fit the equation at available data points. This bias is explained by the recent study of frequency principle (Xu et al., (2019) [17] and Zhang et al., (2019) [11, 19]). In addition to the similarity between the traditional numerical methods and DNNs in the approximation perspective, our work shows that the implicit bias in the learning process, which is different from traditional numerical methods, could help better understand the characteristics of DNNs.
翻译:本文旨在研究Ritz- Galerkin (R-G) 方法与深神经网络(DNN) 方法在解决部分差异方程(PDEs) 和深度神经网络(DNN) 方法(DNN) 方法在解决部分差异方程(PDEs) 和深度神经网络(DNN) 方法(DNN) 的区别,以便更好地了解深层学习。 为此,我们考虑解决一个特定的Poisson问题,即方程的右侧信息只能在n抽样点(即,f在有限的抽样点为人所知 ) 中提供。通过理论和数字研究,我们发现RG方法的解决方案在单维度(1D) 或高维问题下常规性(DNN) 的问题或函数中,与高维度问题(DNNPs) 相类似。 在同一背景下,DNNS 学会一个相对平滑的解决方案,而不管其维度如何,这就是,DNNS 隐含的偏向性功能偏向所有功能中都适合现有数据点的方方方方格。 这种偏差原则(Xuu等人(2019 [17] ) 和Zhang 等人等人等人 (2019、19、19、19、19 19 19 19、19 19 19 19 19 19 19) 和DNNP) 和D 和19 19) 的类似,除了从传统偏差法的类似外, 外, 外,我们的工作还表明的偏向性方法可以帮助从传统偏差性研究外, 外, 外,我们的L 工作显示更接近于传统偏差性学方法。