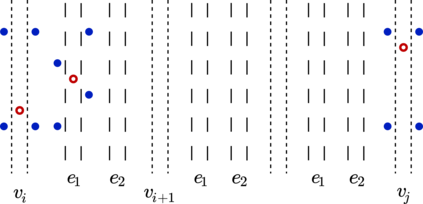
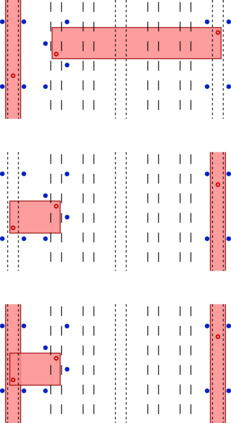
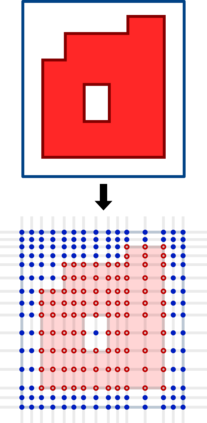
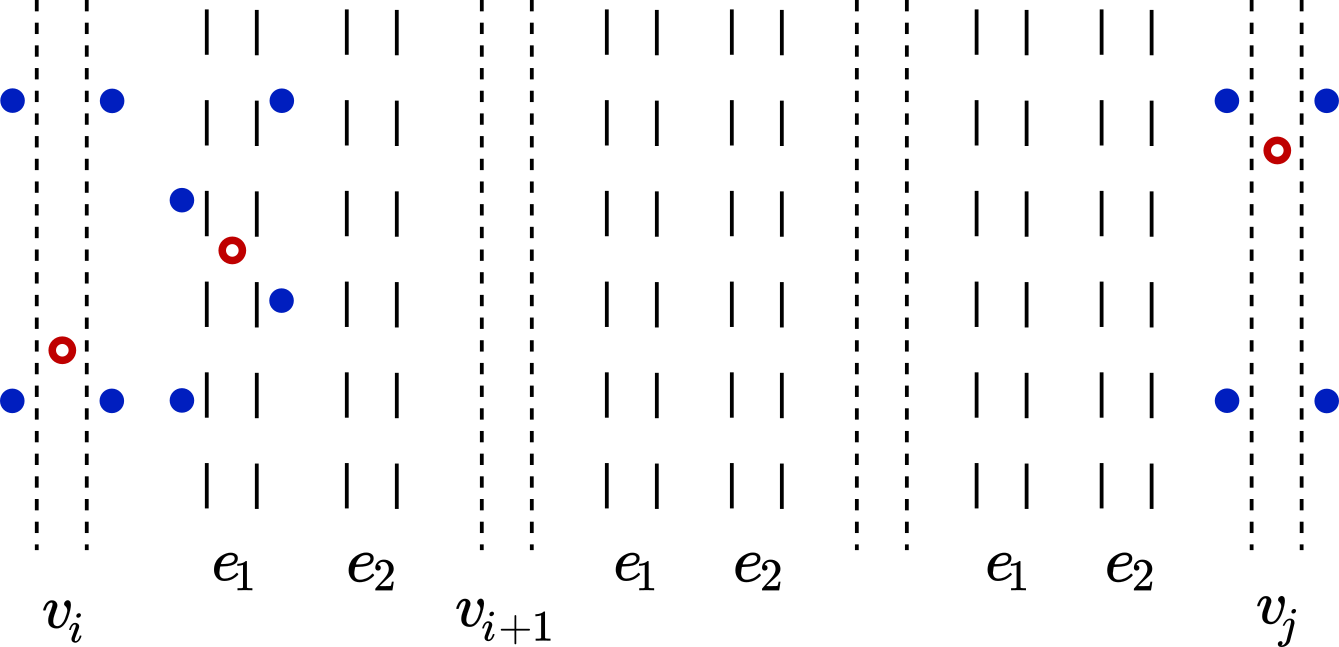
Bereg et al. (2012) introduced the Boxes Class Cover problem, which has its roots in classification and clustering applications: Given a set of n points in the plane, each colored red or blue, find the smallest cardinality set of axis-aligned boxes whose union covers the red points without covering any blue point. In this paper we give an alternative proof of APX-hardness for this problem, which also yields an explicit lower bound on its approximability. Our proof also directly applies when restricted to sets of points in general position and to the case where so-called half-strips are considered instead of boxes, which is a new result. We also introduce a symmetric variant of this problem, which we call Simultaneous Boxes Class Cover and can be stated as follows: Given a set S of n points in the plane, each colored red or blue, find the smallest cardinality set of axis-aligned boxes which together cover S such that all boxes cover only points of the same color and no box covering a red point intersects a box covering a blue point. We show that this problem is also APX-hard and give a polynomial-time constant-factor approximation algorithm.
翻译:Bereg等人(2012年)引入了“框类覆盖”问题,其根源在于分类和组群应用:如果在平面上有一组 n点,每个有色红色或蓝色,则找到最小的轴重框,其结合覆盖红点,但不覆盖任何蓝色点。在本文中,我们为这一问题提供了APX-硬度的替代证明,其相近性也产生一个明显的较低约束。当我们的证据还直接适用于限制在一般位置的一组点,以及所谓半点被考虑而不是箱的情况,这是一个新的结果。我们还引入了这一问题的一个对称变量,我们称之为“同质箱”类,并可以说明如下:如果在平面上有一组 n点,每个有色或蓝色的,则找到最小的轴重点组合组合,从而所有框仅覆盖同一颜色的点,而没有包含一个红点的交叉点,覆盖一个蓝点的框。我们显示,这一问题也是 APX-hard和给一个聚度常数的矩阵。