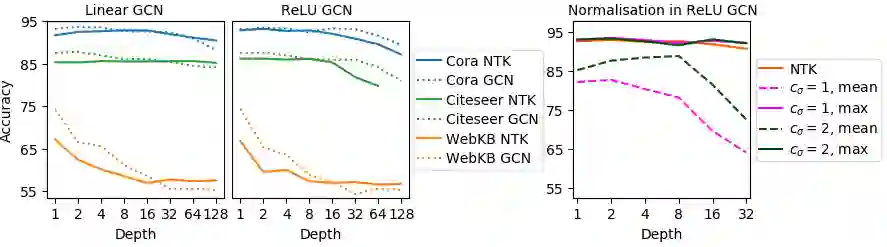
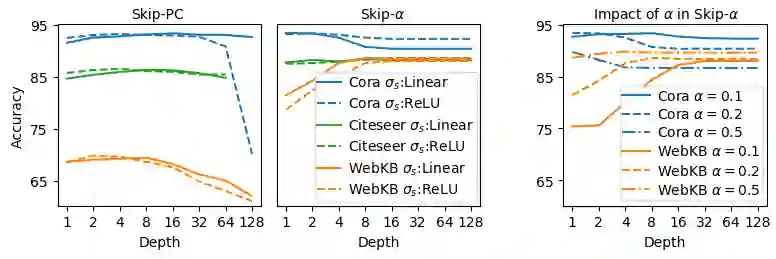
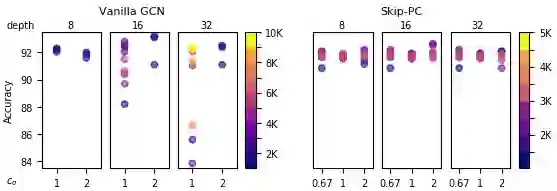
Graph Convolutional Networks (GCNs) have emerged as powerful tools for learning on network structured data. Although empirically successful, GCNs exhibit certain behaviour that has no rigorous explanation -- for instance, the performance of GCNs significantly degrades with increasing network depth, whereas it improves marginally with depth using skip connections. This paper focuses on semi-supervised learning on graphs, and explains the above observations through the lens of Neural Tangent Kernels (NTKs). We derive NTKs corresponding to infinitely wide GCNs (with and without skip connections). Subsequently, we use the derived NTKs to identify that, with suitable normalisation, network depth does not always drastically reduce the performance of GCNs -- a fact that we also validate through extensive simulation. Furthermore, we propose NTK as an efficient `surrogate model' for GCNs that does not suffer from performance fluctuations due to hyper-parameter tuning since it is a hyper-parameter free deterministic kernel. The efficacy of this idea is demonstrated through a comparison of different skip connections for GCNs using the surrogate NTKs.
翻译:图形革命网络(GCN)已成为在网络结构数据上学习的强大工具。虽然在经验上是成功的,但GCN表现出某些没有严格解释的行为 -- -- 例如,GCN的表现随着网络深度的提高而大幅下降,而随着深度的提高,它则略有改善。本文侧重于在图表上进行半监督的学习,并通过神经中枢(NTKs)的透镜解释上述观察。我们从无孔不入的GCN(有和没有跳过连接)中得出相应的NTKs。随后,我们利用派生的NTKs发现,在适当正常化的情况下,网络深度并不总是大幅度降低GCNs的表现 -- -- 我们也通过广泛的模拟来验证这一事实。此外,我们建议NTK是GCNs的一个高效的“升降模型”,它不会因超参数调幅而受到影响,因为它是一个超参数自由的确定性能内核核心。我们通过对GCNs使用子的顶端连接进行对比来证明这一想法的功效。