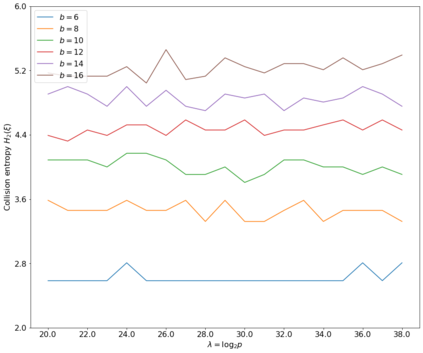
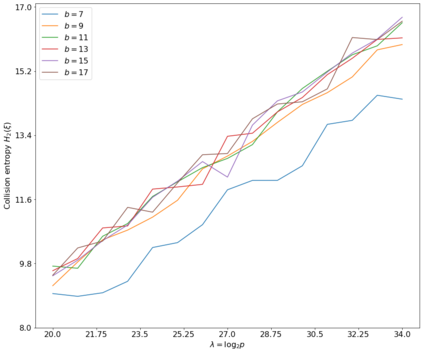
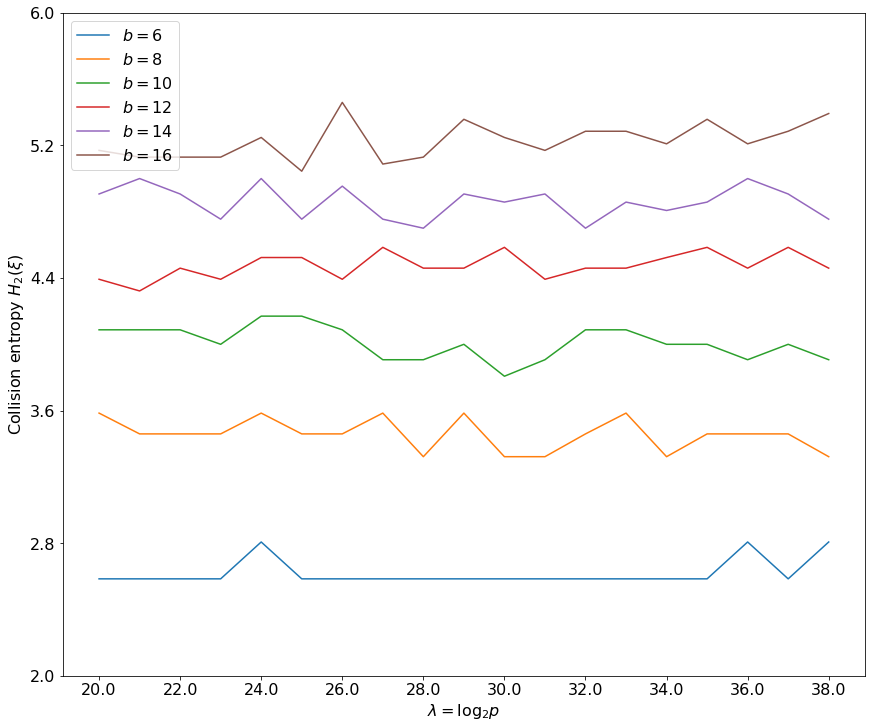
By analogy with the developed cryptographic theory of discrete logarithm problems, we define several hard problems in Entropoid based cryptography, such as Discrete Entropoid Logarithm Problem (DELP), Computational Entropoid Diffie-Hellman problem (CEDHP), and Decisional Entropoid Diffie-Hellman Problem (DEDHP). We post a conjecture that DEDHP is hard in Sylow $q$-subquasigroups. Next, we instantiate an entropoid Diffie-Hellman key exchange protocol. Due to the non-commutativity and non-associativity, the entropoid based cryptographic primitives are supposed to be resistant to quantum algorithms. At the same time, due to the proposed succinct notation for the power indices, the communication overhead in the entropoid based Diffie-Hellman key exchange is very low: for 128 bits of security, 64 bytes in total are communicated in both directions, and for 256 bits of security, 128 bytes in total are communicated in both directions. Our final contribution is in proposing two entropoid based digital signature schemes. The schemes are constructed with the Fiat-Shamir transformation of an identification scheme which security relies on a new hardness assumption: computing roots in finite entropoids is hard. If this assumption withstands the time's test, the first proposed signature scheme has excellent properties: for the classical security levels between 128 and 256 bits, the public and private key sizes are between 32 and 64, and the signature sizes are between 64 and 128 bytes. The second signature scheme reduces the finding of the roots in finite entropoids to computing discrete entropoid logarithms. In our opinion, this is a safer but more conservative design, and it pays the price in doubling the key sizes and the signature sizes. We give a proof-of-concept implementation in SageMath 9.2 for all proposed algorithms and schemes in an appendix.
翻译:与已开发的离散对数问题的加密理论类比, 我们定义了基于 Entoropotime 的加密方法中的若干难题, 如 Discrete Entoroporid Logalatim 问题( DELP ), computurational Entoproid Diffie- Hellman 问题( CEDHP ), 和Decisional Entoprotoid Diffie- Hellman 问题( DEDHP 问题( DEDHP ) 。 我们将DEDEDHP 在 Sylow $q$- subqualsisia 类s 类中很难入调。 其次, 我们即时端点, Diffie- Hellman 关键交换中总共将64个位位数转换为Diffie- Hellman 关键交换 。 由于非通称性能性能和256个位的用户键转换方法, 价格法的变换算算算算算算法系统。