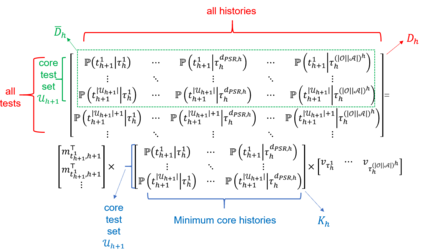
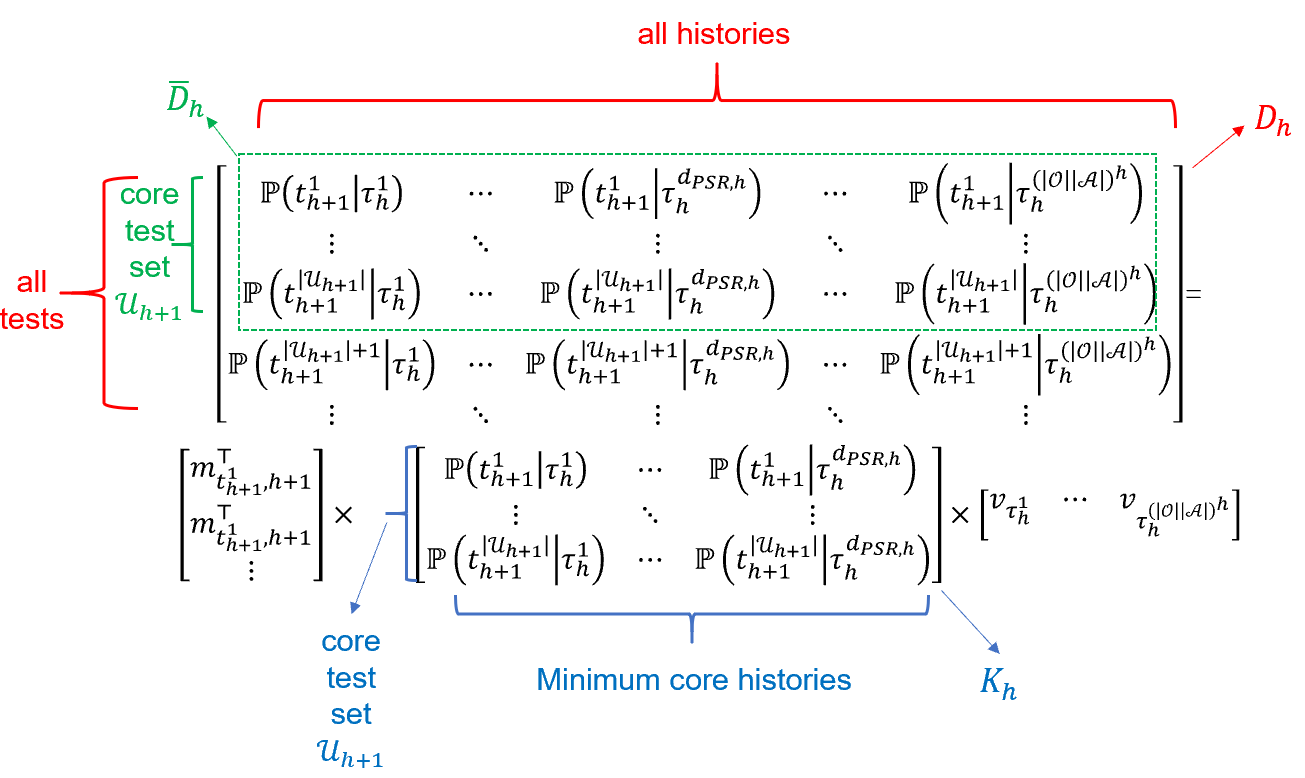
In this paper we study online Reinforcement Learning (RL) in partially observable dynamical systems. We focus on the Predictive State Representations (PSRs) model, which is an expressive model that captures other well-known models such as Partially Observable Markov Decision Processes (POMDP). PSR represents the states using a set of predictions of future observations and is defined entirely using observable quantities. We develop a novel model-based algorithm for PSRs that can learn a near optimal policy in sample complexity scaling polynomially with respect to all the relevant parameters of the systems. Our algorithm naturally works with function approximation to extend to systems with potentially large state and observation spaces. We show that given a realizable model class, the sample complexity of learning the near optimal policy only scales polynomially with respect to the statistical complexity of the model class, without any explicit polynomial dependence on the size of the state and observation spaces. Notably, our work is the first work that shows polynomial sample complexities to compete with the globally optimal policy in PSRs. Finally, we demonstrate how our general theorem can be directly used to derive sample complexity bounds for special models including $m$-step weakly revealing and $m$-step decodable tabular POMDPs, POMDPs with low-rank latent transition, and POMDPs with linear emission and latent transition.
翻译:在本文中,我们研究部分可见动态系统中的在线强化学习(RL) 。我们侧重于预测性国家代表模式(PSRs)模型(PSRs),这是一个表达式模型,包含部分可观测的Markov决策程序(POMDP)等其他著名模型。PSR代表了使用一系列未来观测预测并完全使用可观测数量定义的国家。我们为PSRs开发了一个基于模型的新型算法,该算法可以学习在抽样复杂度方面几乎最佳的政策,在系统所有相关参数方面缩放多元性。我们的算法自然与功能近似(PSRs)合作,将功能扩展至具有潜在较大状态和观测空间的系统。我们表明,鉴于一个可实现的模型类别,学习几乎最佳的政策的样本复杂性仅是多元性,没有明显依赖国家和观测空间的大小。我们的工作是第一件显示多元性样本复杂性的工作,以与PSRs的全球最佳政策竞争。最后,我们展示了我们一般的理论和最接近性最弱的模型,包括低层-OM的模型,直接用于为特殊的深度的深度的模型。