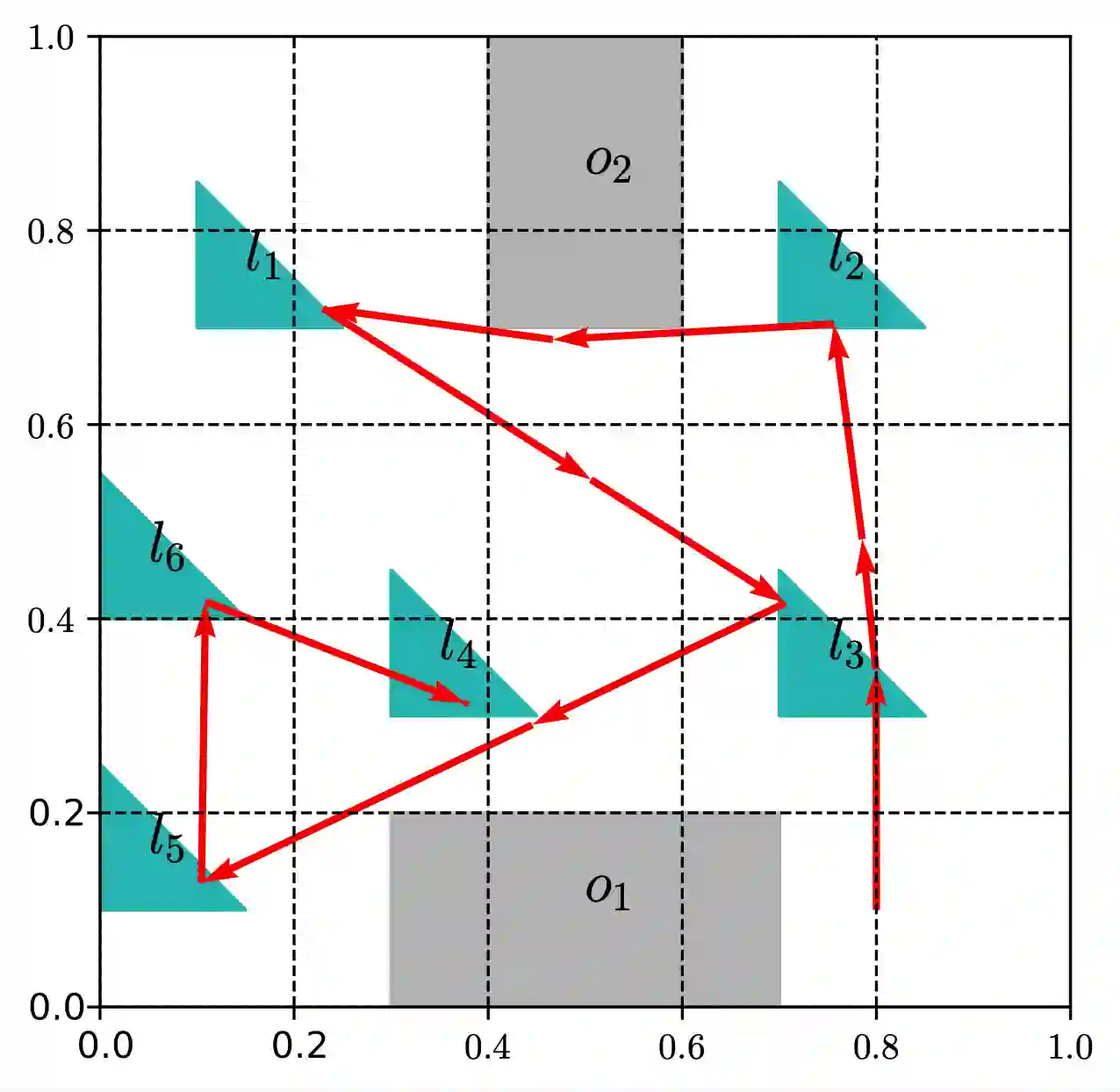
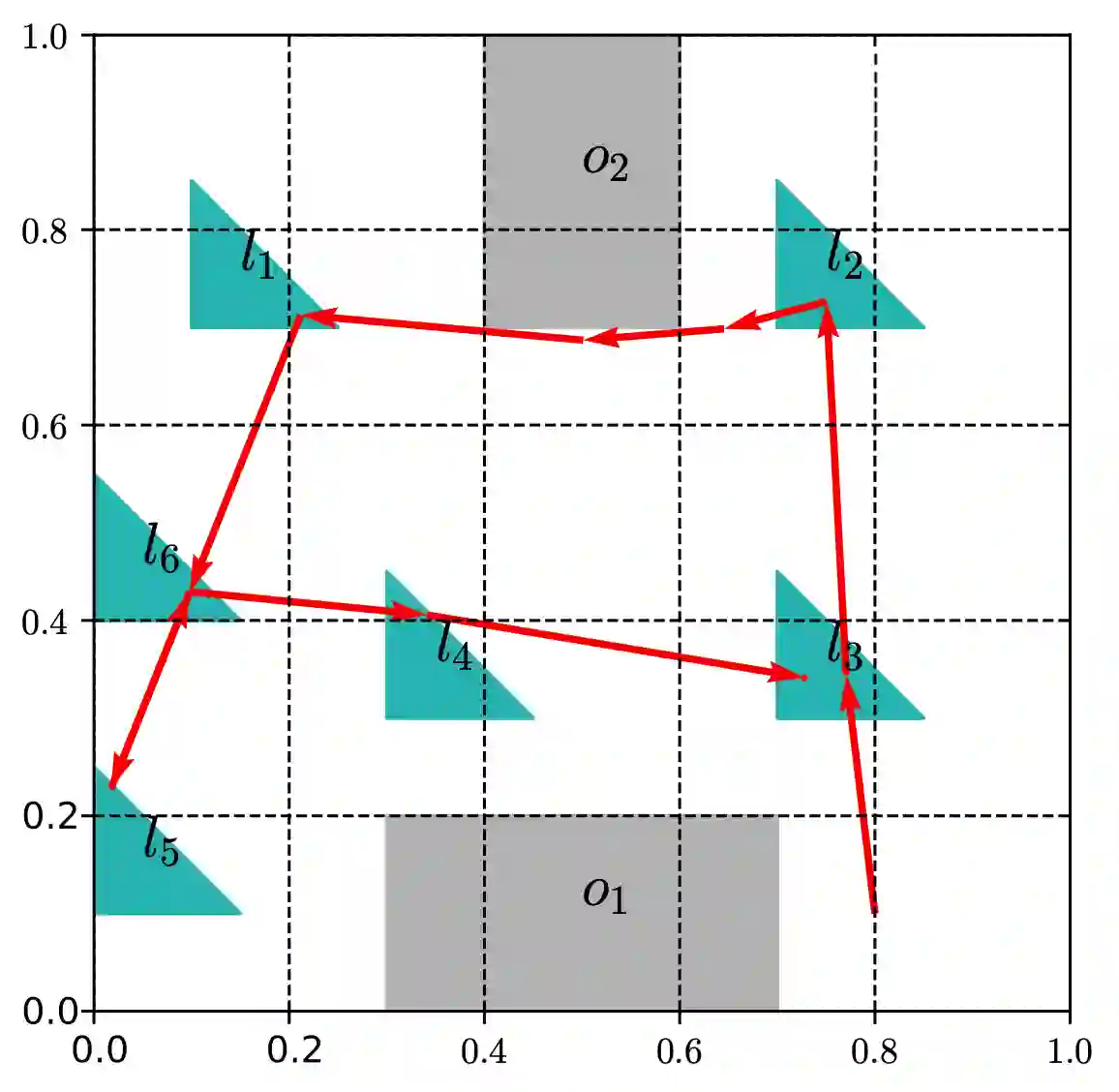
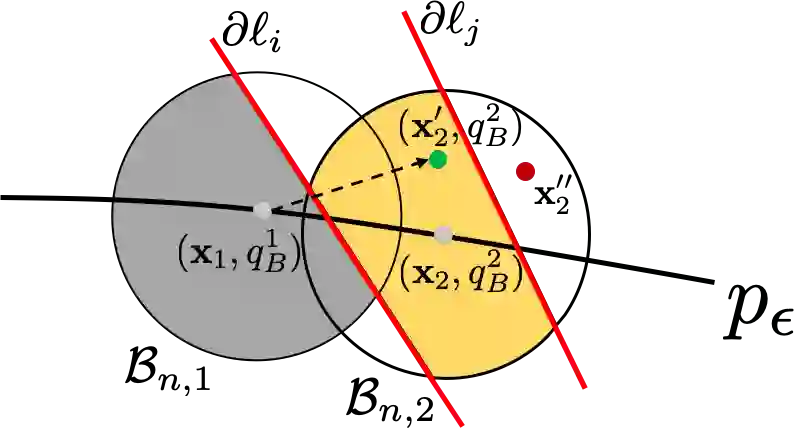
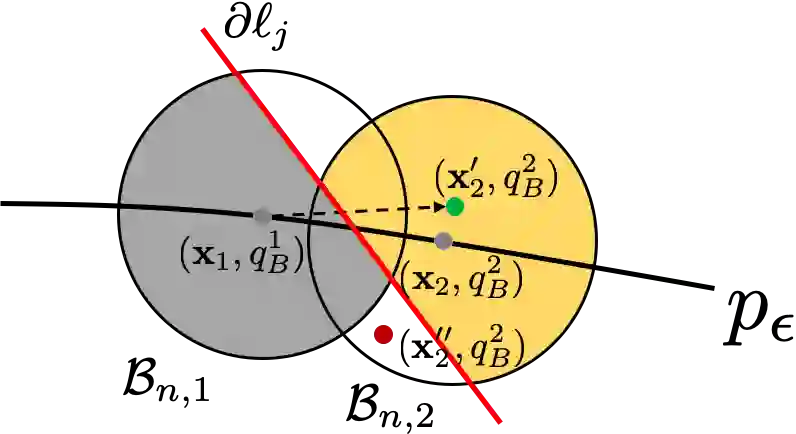
The majority of existing Linear Temporal Logic (LTL) planning methods rely on the construction of a discrete product automaton, that combines a discrete abstraction of robot mobility and a B$\ddot{\text{u}}$chi automaton that captures the LTL specification. Representing this product automaton as a graph and using graph search techniques, optimal plans that satisfy the LTL task can be synthesized. However, constructing expressive discrete abstractions makes the synthesis problem computationally intractable. In this paper, we propose a new sampling-based LTL planning algorithm that does not require any discrete abstraction of robot mobility. Instead, it incrementally builds trees that explore the product state-space, until a maximum number of iterations is reached or a feasible plan is found. The use of trees makes data storage and graph search tractable, which significantly increases the scalability of our algorithm. To accelerate the construction of feasible plans, we introduce bias in the sampling process which is guided by transitions in the B$\ddot{\text{u}}$chi automaton that belong to the shortest path to the accepting states. We show that our planning algorithm, with and without bias, is probabilistically complete and asymptotically optimal. Finally, we present numerical experiments showing that our method outperforms relevant temporal logic planning methods.
翻译:大部分现有的线性时空逻辑(LTL)规划方法都依靠构建离散产品自动图解,该图解将机器人移动的离散抽象和捕获LTL规格的B$dddot=text{u ⁇ $chi 自动图集结合起来。将该产品自动图解作为图表并使用图形搜索技术来代表。然而,构建表达式离散抽象(LTL)的最佳计划可以使合成计算问题变得难以解决。在本文中,我们提出了一个新的基于取样的LTL规划算法,该算法不需要任何离散的机器人移动抽象。相反,它会逐步建立勘探产品状态空间的树,直到达到最大迭代数或找到可行的计划。使用树可以使数据存储和图形搜索具有可调控性,从而大大提高了我们算法的可缩放性。为了加速构建可行的计划,我们在取样过程中引入了偏差,因为B$ddot{{ ⁇ \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\