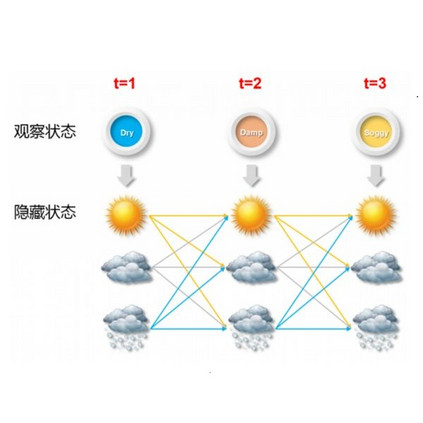
Data sets comprised of sequences of curves sampled at high frequencies in time are increasingly common in practice, but they can exhibit complicated dependence structures that cannot be modelled using common methods of Functional Data Analysis (FDA). We detail a hierarchical approach which treats the curves as observations from a hidden Markov model (HMM). The distribution of each curve is then defined by another fine-scale model which may involve auto-regression and require data transformations using moving-window summary statistics or Fourier analysis. This approach is broadly applicable to sequences of curves exhibiting intricate dependence structures. As a case study, we use this framework to model the fine-scale kinematic movement of a northern resident killer whale (Orcinus orca) off the coast of British Columbia, Canada. Through simulations, we show that our model produces more interpretable state estimation and more accurate parameter estimates compared to existing methods.
翻译:由在高频时间取样的曲线序列组成的数据集在实践中越来越常见,但它们可能表现出复杂的依赖结构,无法使用功能数据分析(FDA)的通用方法进行模拟。我们详细介绍了一种分级方法,将曲线作为隐蔽的Markov模型(HMM)的观测结果。然后,每个曲线的分布由另一个细微模型确定,该模型可能涉及自动反射,需要使用移动式风速摘要统计或Fourier分析进行数据转换。这种方法广泛适用于显示复杂依赖结构的曲线序列。我们通过案例研究,利用这个框架来模拟加拿大不列颠哥伦比亚沿海北部居民虎鲸(Orcinus orca)的细规模运动。我们通过模拟,表明我们的模型产生比现有方法更可解释的状态估计和更准确的参数估计。