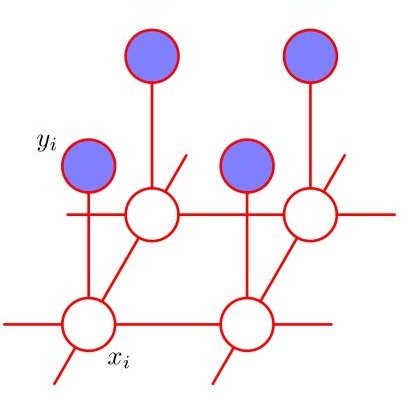
Probabilistic Graphical Models (PGMs) encode conditional dependencies among random variables using a graph -nodes for variables, links for dependencies- and factorize the joint distribution into lower-dimensional components. This makes PGMs well-suited for analyzing complex systems and supporting decision-making. Recent advances in topological signal processing highlight the importance of variables defined on topological spaces in several application domains. In such cases, the underlying topology shapes statistical relationships, limiting the expressiveness of canonical PGMs. To overcome this limitation, we introduce Colored Markov Random Fields (CMRFs), which model both conditional and marginal dependencies among Gaussian edge variables on topological spaces, with a theoretical foundation in Hodge theory. CMRFs extend classical Gaussian Markov Random Fields by including link coloring: connectivity encodes conditional independence, while color encodes marginal independence. We quantify the benefits of CMRFs through a distributed estimation case study over a physical network, comparing it with baselines with different levels of topological prior.
翻译:概率图模型通过图结构编码随机变量间的条件依赖关系——节点表示变量,边表示依赖关系——并将联合分布分解为低维分量,使其适用于分析复杂系统及辅助决策。拓扑信号处理的最新进展凸显了在多个应用领域中定义于拓扑空间上的变量的重要性。在此类情形下,底层拓扑结构塑造了统计关系,限制了经典概率图模型的表达能力。为突破此局限,我们提出了着色马尔可夫随机场,该模型基于霍奇理论,对拓扑空间上高斯边变量的条件依赖与边缘依赖关系进行统一建模。CMRF通过引入边着色机制扩展了经典高斯马尔可夫随机场:连接性编码条件独立性,而着色编码边缘独立性。我们通过物理网络上的分布式估计案例研究量化了CMRF的优势,并与具有不同拓扑先验水平的基线方法进行了对比。